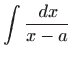 ,
,
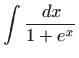 ,
,
![$ \displaystyle\int \frac{\sin \sqrt[3]{x}}{\sqrt[3]{x^{2}}} dx$](img72.gif) ,
,
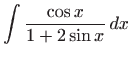 .
.
Izračunajte integrale:
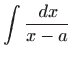 ,
,
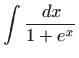 ,
,
![$ \displaystyle\int \frac{\sin \sqrt[3]{x}}{\sqrt[3]{x^{2}}} dx$](img72.gif) ,
,
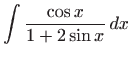 .
.
Rješenje. Integrale računamo svodeći zadani integral na tablični dopustivom zamjenom varijable integracije nekom funkcijom (bijekcijom) ili dopustivom zamjenom nekog analitičkog izraza novom varijablom integracije.
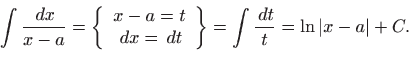
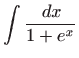 |
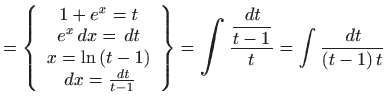 |
|
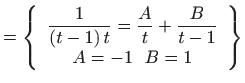 |
||
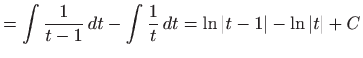 |
||
Osim suspstitucije u ovom zadatku korišten je i rastav na parcijalne
razlomke gdje smo razlomak pod integralom
![]() rastavili na dva jednostavnija.
rastavili na dva jednostavnija.
![$\displaystyle \int \frac{\sin \sqrt[3]{x}}{\sqrt[3]{x^{2}}} dx$](img89.gif) |
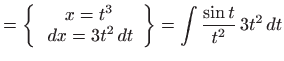 |
|
![$\displaystyle =3\int \sin t dt=-3\cos t+C=-3\cos \sqrt[3]{x}+C.$](img91.gif) |
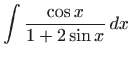 |
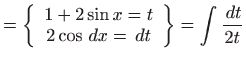 |
|
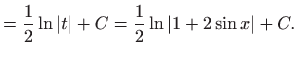 |