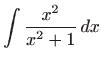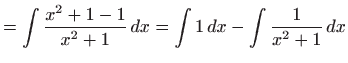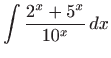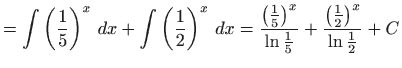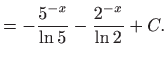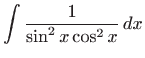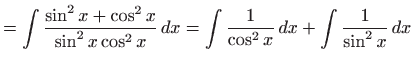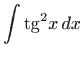☰
matematika2
NEODREĐENI INTEGRAL
NEODREĐENI INTEGRAL
Metode supstitucije
Neposredno integriranje
Izračunajte integrale:
- a)
-
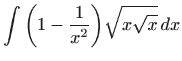 ,
,
- b)
-
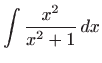 ,
,
- c)
-
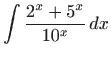 ,
,
- d)
-
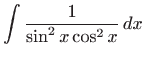 ,
,
- e)
-
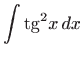 .
.
Rješenje. U računanju primjenjujemo
![[*]](../icons.gif/crossref.gif) [M2, teorem 1.4]1.1 i
tablicu osnovnih integrala
[M2, teorem 1.4]1.1 i
tablicu osnovnih integrala
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 1.1.1].
[M2, poglavlje 1.1.1].
- a)
- Da bismo mogli primjeniti integral potencije iz tablice osnovnih
integrala podintegralu funkciju prvo zapisujemo u jednostavnijem obliku, pa
vrijedi
- b)
- Tablični integral dobivamo nakon što brojniku dodamo i
oduzmemo broj
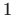 , pa vrijedi
, pa vrijedi
- c)
- Vrijedi
- d)
- Koristeći osnovni trigonometrijski identitet dobivamo
- e)
- Zapisivanjem funkcije
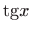 u obliku
u obliku
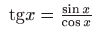 dobivamo
dobivamo
NEODREĐENI INTEGRAL
NEODREĐENI INTEGRAL
Metode supstitucije
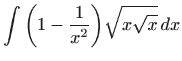 ,
,
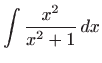 ,
,
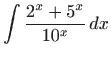 ,
,
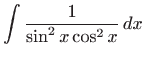 ,
,
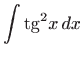 .
.
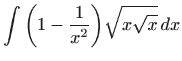 ,
,
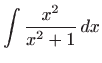 ,
,
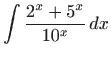 ,
,
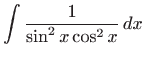 ,
,
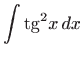 .
.
![]() [M2, teorem 1.4]1.1 i
tablicu osnovnih integrala
[M2, teorem 1.4]1.1 i
tablicu osnovnih integrala
![]() [M2, poglavlje 1.1.1].
[M2, poglavlje 1.1.1].
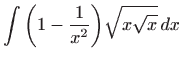
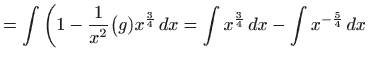
![$\displaystyle =\frac{x^{\frac{7}{4}}}{\frac{7}{4}}-\frac{x^{-\frac{1}{4}}}{-\frac{1}{4}} +C=\frac{4x\sqrt[4]{x^{3}}}{7}+\frac{4}{\sqrt[4]{x}}+C$](img54.gif)
![$\displaystyle =\frac{4\left( x^{2}+7\right) }{7\sqrt[4]{x}}+C.$](img55.gif)