☰
matematika2
Lokalni ekstremi funkcije dviju
FUNKCIJE VIŠE VARIJABLA
Primjena ekstrema, 2. primjer
Primjena ekstrema, 1. primjer
U 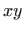 ravnini odredite točku
ravnini odredite točku 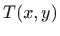 za koju je zbroj kvadrata
udaljenosti od pravaca
za koju je zbroj kvadrata
udaljenosti od pravaca 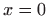 ,
, 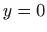 i
i 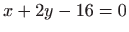 najmanji.
najmanji.
Rješenje.
Neka je 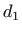 udaljenost točke
udaljenost točke 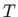 od pravca
od pravca 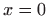 ,
, 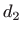 udaljenost
točke
udaljenost
točke 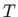 od pravca
od pravca 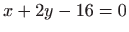 i
i 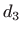 udaljenost točke
udaljenost točke 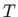 od pravca
od pravca
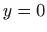 . Tada vrijedi
. Tada vrijedi
Funkcija kojoj trebamo izračunati ekstrem i koja zadaje zbroj kvadrata
udaljenosti točke 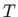 od zadanih pravaca ima oblik
od zadanih pravaca ima oblik
Nakon kvadriranja i stavljanja na zajednički nazivnik funkciju 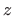 možemo zapisati na sljedeći način
možemo zapisati na sljedeći način
Tražimo ekstreme funkcije 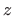 odnosno najprije njene stacionarne točke. U tu svrhu izračunajmo
parcijalne derivacije funkcije
odnosno najprije njene stacionarne točke. U tu svrhu izračunajmo
parcijalne derivacije funkcije 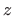 po varijablama
po varijablama 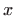 i
i 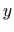 . Vrijedi
. Vrijedi
Rješavanjem sustava jednadžbi
dobivamo stacionarnu točku
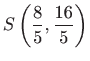 .
.
Budući da parcijalne derivacije drugog reda funkcije 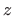 u točki
u točki 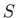 imaju vrijednosti
imaju vrijednosti
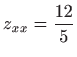 ,
,
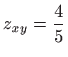 i
i
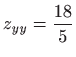 , slijedi
, slijedi
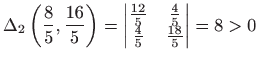
i
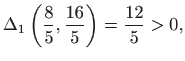
pa je tražena točka minimuma funkcije 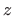 tj.
točka ravnine
tj.
točka ravnine 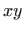 , koja ispunjava uvjete zadatka, točka
, koja ispunjava uvjete zadatka, točka
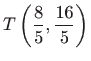 .
.
Lokalni ekstremi funkcije dviju
FUNKCIJE VIŠE VARIJABLA
Primjena ekstrema, 2. primjer
![]() ravnini odredite točku
ravnini odredite točku ![]() za koju je zbroj kvadrata
udaljenosti od pravaca
za koju je zbroj kvadrata
udaljenosti od pravaca ![]() ,
, ![]() i
i ![]() najmanji.
najmanji.
![]() udaljenost točke
udaljenost točke ![]() od pravca
od pravca ![]() ,
, ![]() udaljenost
točke
udaljenost
točke ![]() od pravca
od pravca ![]() i
i ![]() udaljenost točke
udaljenost točke ![]() od pravca
od pravca
![]() . Tada vrijedi
. Tada vrijedi
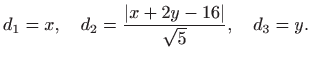
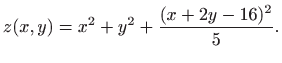
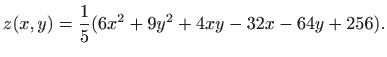
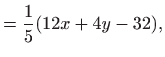
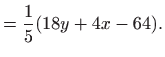
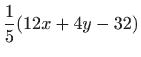
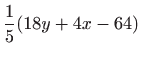
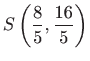 .
.
![]() u točki
u točki ![]() imaju vrijednosti
imaju vrijednosti
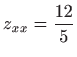 ,
,
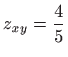 i
i
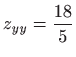 , slijedi
, slijedi
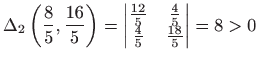 i
i 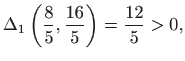
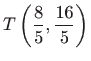 .
.