Odredite lokalne ekstreme funkcija:
Rje┼Īenje.
Lokalne ekstreme odre─æivat ─ćemo prema postupku opisanom u
![]() [M2, poglavlje 3.10].
[M2, poglavlje 3.10].
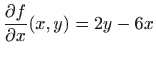 i i 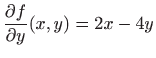 . . |
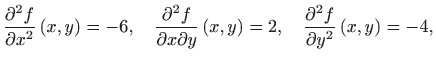 |
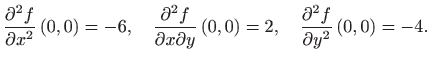 |
Determinanta
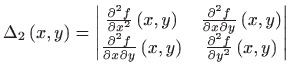
u to─Źki
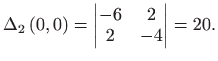
Kako je
![]() i
i
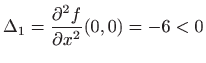 zaklju─Źujemo da zadana
funkcija u to─Źki
zaklju─Źujemo da zadana
funkcija u to─Źki
![]() posti┼Še maksimalnu vrijednost
posti┼Še maksimalnu vrijednost
![]() (slika 3.8).
(slika 3.8).
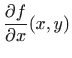 |
||
 |
Da bismo provjerili dovoljne uvjete za dobivene to─Źke odredit µemo parcijalne derivacije drugog reda funkcije ![]() . Vrijedi
. Vrijedi
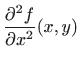 |
||
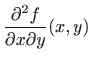 |
||
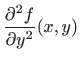 |
Za to─Źku
![]() je
je
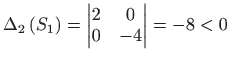 pa, prema
pa, prema
![]() [M2, teorem 3.8],
u to─Źki
[M2, teorem 3.8],
u to─Źki ![]() funkcija
funkcija ![]() nema ekstrem.
nema ekstrem.
Za to─Źku ![]() vrijedi
vrijedi
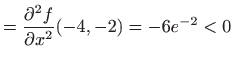 i i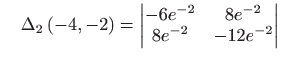 |
||