☰
matematika2
Zadaci za vježbu
FUNKCIJE VIŠE VARIJABLA
VIŠESTRUKI INTEGRALI
Rješenja zadataka za vježbu
- 1.
- a)
-
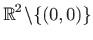 ,
,
- b)
-
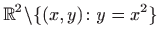 ,
,
- c)
-
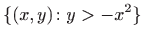 ,
,
- d)
-
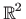 ,
,
- e)
-
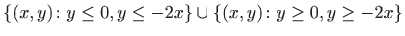 ,
,
- f)
-
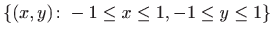 ,
,
- g)
-
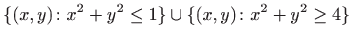 ,
,
- h)
-
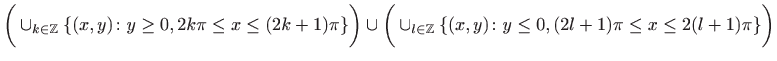 ,
,
- i)
-
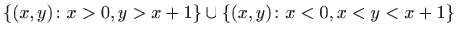 .
.
- 2.
- a)
-
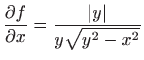 ,
,
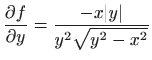 ,
,
- b)
-
 ,
,
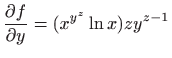 ,
,
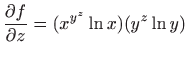 .
.
- 3.
- a)
-
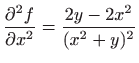 ,
,
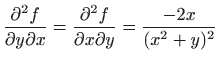 ,
,
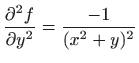 ,
,
- b)
-
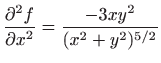 ,
,
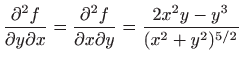 ,
,
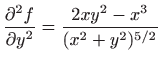 .
.
- 4.
-
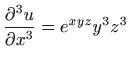 ,
,
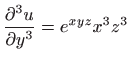 ,
,
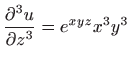 .
.
- 5.
-
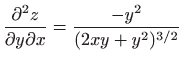 .
.
- 6.
-
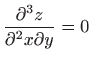 .
.
- 7.
-
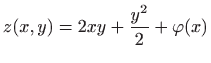 .
.
- 8.
-
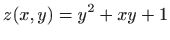 .
.
- 9.
-
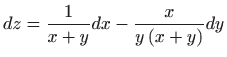 .
.
- 10.
-
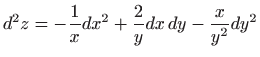 .
.
- 11.
- a)
-
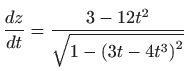 ,
,
- b)
-
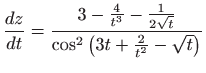 .
.
- 12.
- a)
-
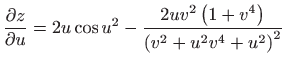 ,
,
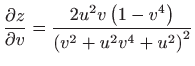 ,
,
- b)
-
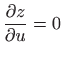 ,
,
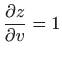 .
.
- 13.
-
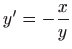 ,
,
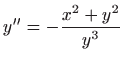 .
.
- 14.
-
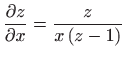 ,
,
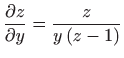 .
.
- 15.
-
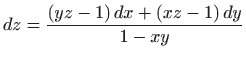 .
.
- 16.
-
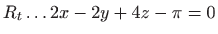 ,
,
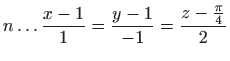 .
.
- 17.
- Lokalni minimum je u točki
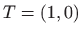 .
.
- 18.
- Lokalni maksimum je u točki
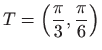 .
.
- 19.
-
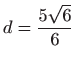 .
.
- 20.
-
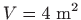 .
.
- 21.
- Lokalni minimum je u točki
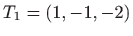 , a lokalni maksimum je u
točki
, a lokalni maksimum je u
točki
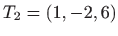 .
.
- 22.
-
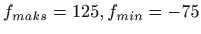 .
.
- 23.
- Minimum je u točki
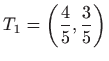 , a
maksimum je u točki
, a
maksimum je u točki
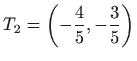 .
.
- 24.
-
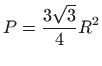 .
.
- 25.
- Najmanje udaljena točka je
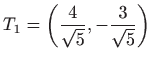 , a najviše
udaljena točka je
, a najviše
udaljena točka je
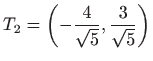 .
.
- 26.
- Minimum je u točki
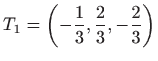 ,
maksimum je u
,
maksimum je u
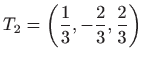 .
.
- 27.
- Nema ekstrema u točki
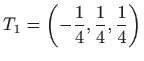 .
.
- 28.
-
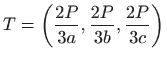 .
.
Zadaci za vježbu
FUNKCIJE VIŠE VARIJABLA
VIŠESTRUKI INTEGRALI
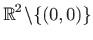 ,
,
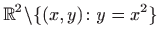 ,
,
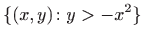 ,
,
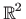 ,
,
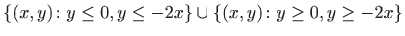 ,
,
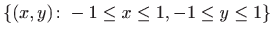 ,
,
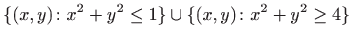 ,
,
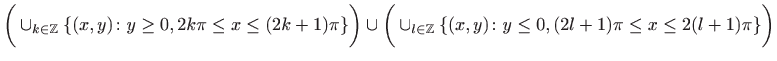 ,
,
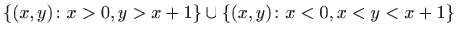 .
.
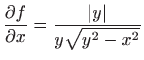 ,
,
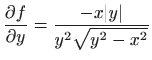 ,
,
 ,
,
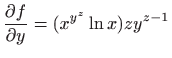 ,
,
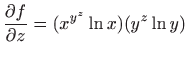 .
.
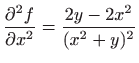 ,
,
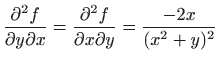 ,
,
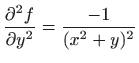 ,
,
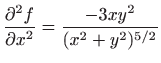 ,
,
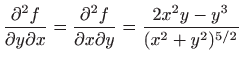 ,
,
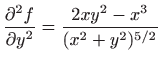 .
.
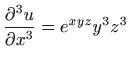 ,
,
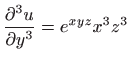 ,
,
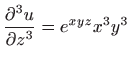 .
.
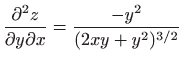 .
.
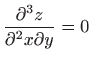 .
.
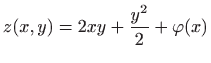 .
.
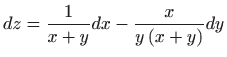 .
.
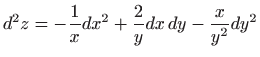 .
.
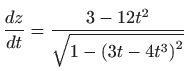 ,
,
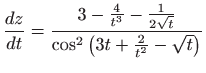 .
.
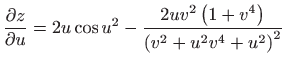 ,
,
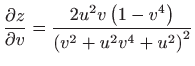 ,
,
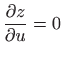 ,
,
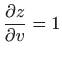 .
.
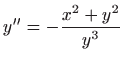 .
.
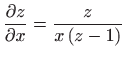 ,
,
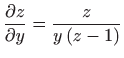 .
.
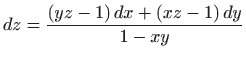 .
.
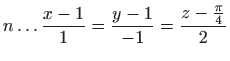 .
.
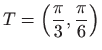 .
.
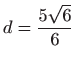 .
.
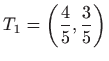 , a
maksimum je u točki
, a
maksimum je u točki
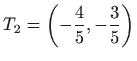 .
.
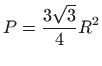 .
.
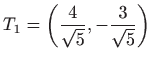 , a najviše
udaljena točka je
, a najviše
udaljena točka je
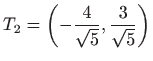 .
.
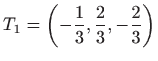 ,
maksimum je u
,
maksimum je u
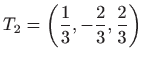 .
.
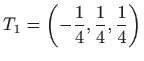 .
.
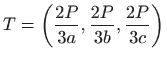 .
.