☰
matematika2
Primjena vezanog ekstrema, 2.
FUNKCIJE VIé E VARIJABLA
RjeéÀenja zadataka za vjeéƒbu
Zadaci za vjeéƒbu
- 1.
- Odredite i skicirajte podruáje definicije funkcija:
- a)
-
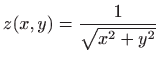 ,
,
- b)
-
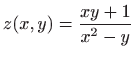 ,
,
- c)
-
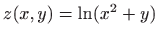 ,
,
- d)
-
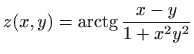 ,
,
- e)
-
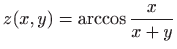 ,
,
- f)
-
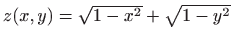 ,
,
- g)
-
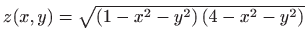 ,
,
- h)
-
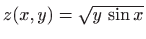 ,
,
- i)
-
![$ z(x,y)=\displaystyle \ln\left[x \ln(y-x)\right]$](img1087.gif) .
.
- 2.
- Odredite parcijalne derivacije prvog reda funkcija:
- a)
-
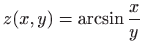 ,
,
- b)
-
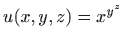 .
.
- 3.
- Odredite parcijalne derivacije drugog reda funkcija:
- a)
-
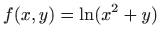 ,
,
- b)
-
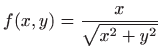 .
.
- 4.
- Za funkciju
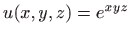 odredite
odredite
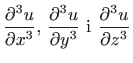 .
.
- 5.
- Odredite
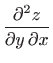 , ako je
, ako je
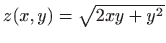 .
.
- 6.
- Odredite
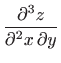 , ako je
, ako je
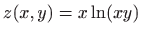 .
.
- 7.
- RijeéÀite parcijalnu diferencijalnu jednadéƒbu
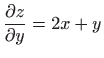 .
.
- 8.
- RijeéÀite parcijalnu diferencijalnu jednadéƒbu
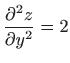 uz uvjete
uz uvjete
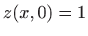 i
i
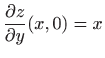 .
.
- 9.
- Odredite totalni diferencijal prvog reda funkcije
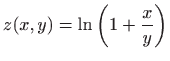 .
.
- 10.
- Odredite totalni diferencijal drugog reda funkcije
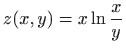 .
.
- 11.
- Odredite derivaciju
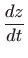 ako je:
ako je:
- a)
-
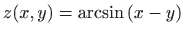 ,
, 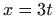 ,
, 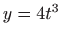 ,
,
- b)
-
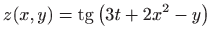 ,
,
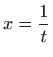 ,
,
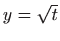 .
.
- 12.
- Odredite parcijalne derivacije
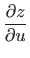 i
i
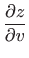 ako je:
ako je:
- a)
-
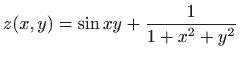 ,
, 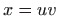 ,
,
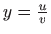 ,
,
- b)
-
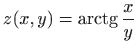 ,
, 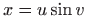 ,
, 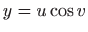 .
.
- 13.
- Odredite derivaciju prvog i drugog reda funkcije
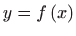 zadane implicitno sa
zadane implicitno sa
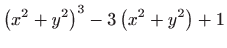 .
.
- 14.
- Odredite parcijalne derivacije prvog reda funkcije
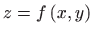 zadane implicitno sa
zadane implicitno sa
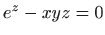 .
.
- 15.
- Odredite totalni diferencijal prvog reda funkcije
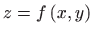 zadane implicitno s
zadane implicitno s
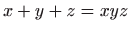 .
.
- 16.
- Odredite tangencijalnu ravninu i normalu na plohu
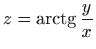 u toáki
u toáki
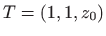 .
.
- 17.
- Odredite lokalne ekstreme funkcije
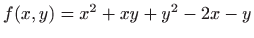 .
.
- 18.
- Odredite lokalne ekstreme funkcije
- a)
-
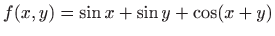 za
za
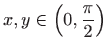 ,
,
- b)
-
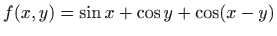 za
za
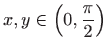 .
.
- 19.
- Izraáunajte najkraáu udaljenost toáke
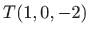 do ravnine
do ravnine 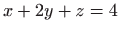 .
.
- 20.
- Kutija bez poklopca treba se napraviti od
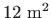 kartona. Izraáunajte maksimalan volumen takve
kutije.
kartona. Izraáunajte maksimalan volumen takve
kutije.
- 21.
- Odredite lokalne ekstreme funkcije
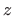 zadane
implicitno s
zadane
implicitno s
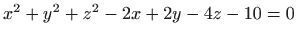 .
.
- 22.
- Odredite najveáu i najmanju vrijednost funkcije
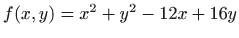 ako je
ako je
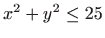 .
.
- 23.
- Odredite ekstreme funkcije
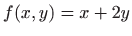 uz uvjet
uz uvjet 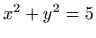 .
.
- 24.
- Pomoáu uvjetnih ekstrema odredite maksimalnu
povréÀinu jednakokraánog trokuta upisanog u
kruƒnicu polumjera
 .
.
- 25.
- Na elipsi
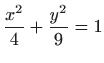 odredite toáke koje su najmanje i najviéÀe udaljene od
pravca
odredite toáke koje su najmanje i najviéÀe udaljene od
pravca 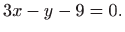
- 26.
- Odredite ekstreme funkcije
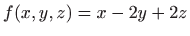 uz uvjet
uz uvjet
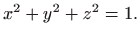
- 27.
- Odredite ekstreme funkcije
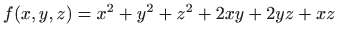 uz uvjet
uz uvjet
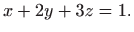
- 28.
- U trokutu
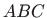 povréÀine
povréÀine 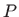 i stranica
i stranica 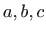 odredite
toáku
odredite
toáku 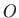 takvu da je produkt udaljenosti te toáke do
stranica trokuta maksimalan.
takvu da je produkt udaljenosti te toáke do
stranica trokuta maksimalan.
Primjena vezanog ekstrema, 2.
FUNKCIJE VIé E VARIJABLA
RjeéÀenja zadataka za vjeéƒbu
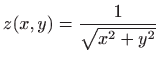 ,
,
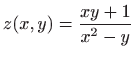 ,
,
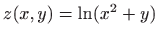 ,
,
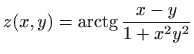 ,
,
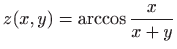 ,
,
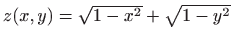 ,
,
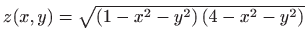 ,
,
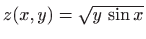 ,
,
![$ z(x,y)=\displaystyle \ln\left[x \ln(y-x)\right]$](img1087.gif) .
.
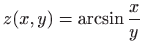 ,
,
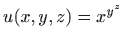 .
.
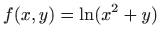 ,
,
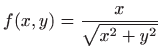 .
.
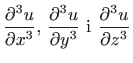 .
.
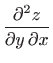 , ako je
, ako je
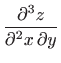 , ako je
, ako je
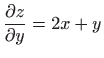 .
.
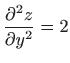 uz uvjete
uz uvjete
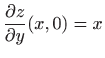 .
.
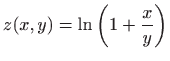 .
.
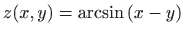 ,
, 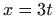 ,
, 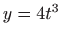 ,
,
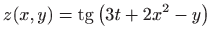 ,
,
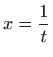 ,
,
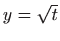 .
.
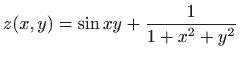 ,
, 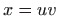 ,
,
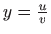 ,
,
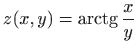 ,
, 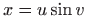 ,
, 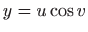 .
.
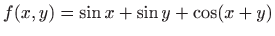 za
za
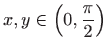 ,
,
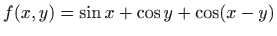 za
za
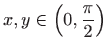 .
.
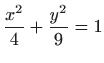 odredite toáke koje su najmanje i najviéÀe udaljene od
pravca
odredite toáke koje su najmanje i najviéÀe udaljene od
pravca