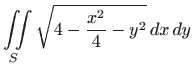 izrazite u eliptičkim
koordinatama. Izračunajte integral ako je
izrazite u eliptičkim
koordinatama. Izračunajte integral ako je 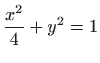 i
i
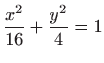 u prvom
kvadrantu.
u prvom
kvadrantu.
Integral
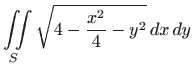 izrazite u eliptičkim
koordinatama. Izračunajte integral ako je
izrazite u eliptičkim
koordinatama. Izračunajte integral ako je ![]() dio prstena omeđen elipsama
dio prstena omeđen elipsama
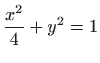 i
i
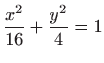 u prvom
kvadrantu.
u prvom
kvadrantu.
Rješenje.
Područje integracije ![]() prikazano je na Slici 4.5.
Uvedimo nove varijable
prikazano je na Slici 4.5.
Uvedimo nove varijable ![]() i
i ![]() supstitucijom
supstitucijom
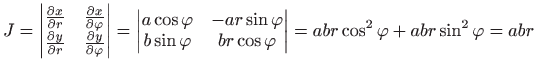 |
Trebamo pronaći jednadžbe dviju rubnih elipsa u novim, eliptičkim koordinatama:
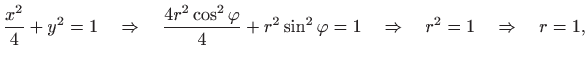 |
|
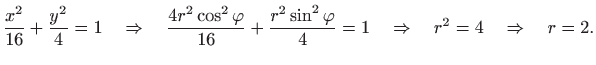 |
 |
 |
|
 |
||
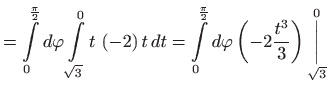 |
||
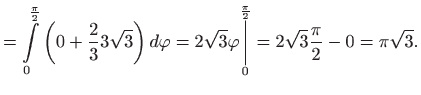 |