☰
matematika2
Eliptične koordinate u dvostrukom
VIŠESTRUKI INTEGRALI
Volumen tijela, 1. primjer
Površina ravninskog lika
Izračunajte površinu lika
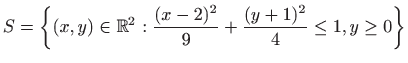 . . |
|
Rješenje.
Površina područja 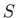 , prema
, prema
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 4.2.1], računa se po formuli
[M2, poglavlje 4.2.1], računa se po formuli
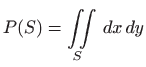 . . |
|
Slika:
Područje integracije
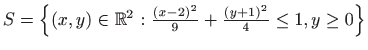 .
.
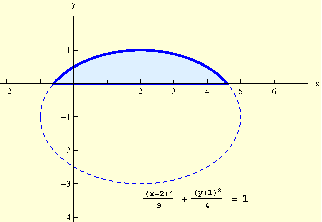 |
Budući je područje 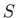 (slika 4.6) određeno pravcem i
elipsom koja nije centralna, prijeđimo na eliptične koordinate u pomaknutom koordinatnom sustavu:
(slika 4.6) određeno pravcem i
elipsom koja nije centralna, prijeđimo na eliptične koordinate u pomaknutom koordinatnom sustavu:
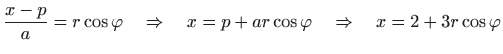 , , |
|
odnosno
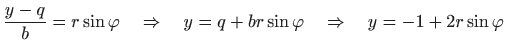 . . |
|
Za ovakvu zamjenu varijabli Jakobijan je 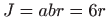 pa je
pa je
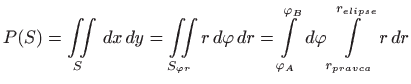 . . |
|
Jednadžba elipse je
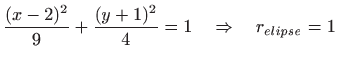 , , |
|
a jednadžba pravca je
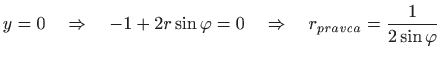 . . |
|
Još nam trebaju granične vrijednosti za 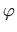 .
Izračunajmo najprije presječne točke
.
Izračunajmo najprije presječne točke 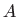 i
i 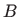 elipse i pravca.
Dobijemo ih rješavanjem sustava
elipse i pravca.
Dobijemo ih rješavanjem sustava
Iz
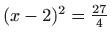 slijedi
slijedi
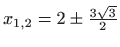 ,
pa su presječne točke
,
pa su presječne točke
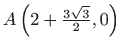 i
i
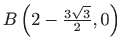 .
Za vrijednosti
.
Za vrijednosti
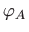 i
i
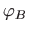 vrijedi
vrijedi
Primijetimo da vrijednosti
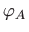 i
i
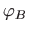 nisu kutovi koje dužine
nisu kutovi koje dužine
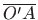 odnosno
odnosno
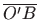 zatvaraju s pozitivnim dijelom osi
zatvaraju s pozitivnim dijelom osi
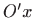 .
Sada je
.
Sada je
Eliptične koordinate u dvostrukom
VIŠESTRUKI INTEGRALI
Volumen tijela, 1. primjer
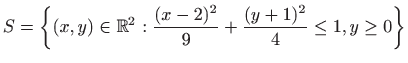 .
.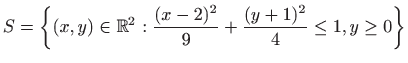 .
.![]() , prema
, prema
![]() [M2, poglavlje 4.2.1], računa se po formuli
[M2, poglavlje 4.2.1], računa se po formuli
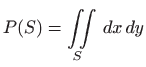 .
.![]() (slika 4.6) određeno pravcem i
elipsom koja nije centralna, prijeđimo na eliptične koordinate u pomaknutom koordinatnom sustavu:
(slika 4.6) određeno pravcem i
elipsom koja nije centralna, prijeđimo na eliptične koordinate u pomaknutom koordinatnom sustavu:
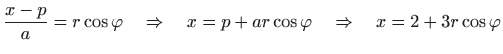 ,
,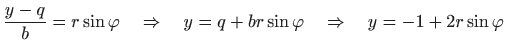 .
.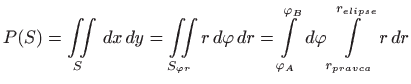 .
.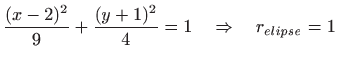 ,
,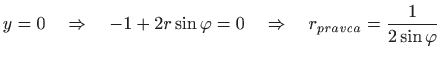 .
.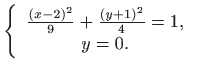
![]() slijedi
slijedi
![]() ,
pa su presječne točke
,
pa su presječne točke
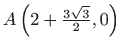 i
i
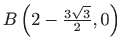 .
Za vrijednosti
.
Za vrijednosti
![]() i
i
![]() vrijedi
vrijedi
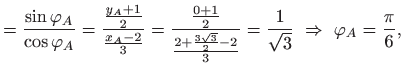
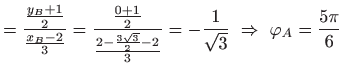 .
.![]() i
i
![]() nisu kutovi koje dužine
nisu kutovi koje dužine
![]() odnosno
odnosno
![]() zatvaraju s pozitivnim dijelom osi
zatvaraju s pozitivnim dijelom osi
![]() .
Sada je
.
Sada je
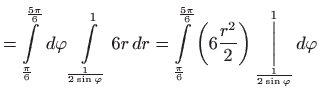
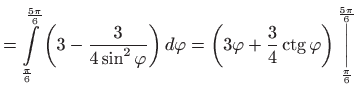
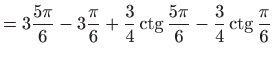
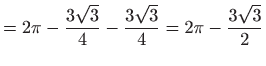 .
.