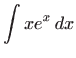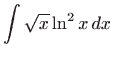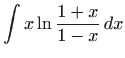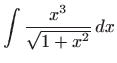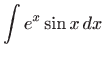×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Uvođenje novog argumenta     NEODREĐENI INTEGRAL     Rekurzivne formule

Metoda parcijalne integracije

Izračunajte integrale:

a)

$$\int xe^{x} dx$$ ,

b)

$$\int \sqrt{x}\ln ^{2}x dx$$ ,

c)

$$\int x\ln {\frac{1+x}{1-x}} dx$$ ,

d)

$$\int \frac{x^{3}}{\sqrt{1+x^{2}}} dx$$ ,

e)

$$\int e^{x}\sin x dx$$ .

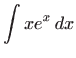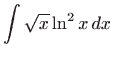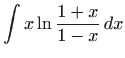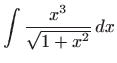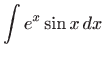Rješenje. U računaju zadanih integrala koristimo formulu parcijalne integracije [M2, teorem 1.7]. Ideja je da integral koji se pojavi nakon parcijalne integracije bude jednostavniji od zadanog integrala.

a)

U parcijalnoj integraciji uzimamo da je $u=x$ i $dv=e^{x} dx$ , jer time $x$ derivacijom postaje $1$ čime se integriranje pojednostavnjuje.

$$\int xe^{x} dx =\left\{ \begin{array}{cc} u=x & dv=e^{x} dx du= dx & v=\int e^{x} dx=e^{x} \end{array} \right\}$$

$$=xe^{x}-\int e^{x} dx=xe^{x}-e^{x}+C=\left( x-1\right) e^{x}+C.$$

b)

Parcijalnu integraciju možemo provoditi i više puta uzastopce, npr. u slijedećem intgralu zadano je $\ln ^{2}x$ , pa nakon dvije parcijelne integracije $\ln$ "nestaje".

$$\int \sqrt{x}\ln ^{2}x dx =\left\{ \begin{array}{cc} u=\ln ^{2}x & dv=\sqrt{x} dx d... ...c{2\ln x}{x} dx & v=\displaystyle \frac{2\sqrt{x^{3}}}{3} \end{array} \right\}$$

$$=\frac{2}{3}\sqrt{x^{3}}\ln ^{2}x-\frac{4}{3}\int \sqrt{x}\ln x ... ...{x} dx du=\frac{ dx}{x} & v=\frac{2\sqrt{x^{3}}}{3} \end{array} \right\}$$

$$=\frac{2}{3}\sqrt{x^{3}}\ln ^{2}x-\frac{4}{3}\left( \frac{2}{3}\sqrt{x^{3}} \ln x-\frac{2}{3}\int \sqrt{x} dx\right)$$

$$=\frac{2}{3}\sqrt{x^{3}}\ln ^{2}x-\frac{8}{9}\sqrt{x^{3}}\ln x+\frac{16}{27 }\sqrt{x^{3}}+C$$

$$=\frac{2}{3}\sqrt{x^{3}}\left( \ln ^{2}x-\frac{4}{3}\ln x+\frac{8}{9} \right) +C.$$

c)

Vrijedi

$$\int x\ln {\frac{1+x}{1-x}} dx =\left\{ \begin{array}{cc} u=\ln {\frac{1+x}{1-x}} & dv=x dx du=\frac{2}{1-x^{2}} dx & v=\frac{x^{2}}{2} \end{array} \right\}$$

$$=\frac{x^{2}}{2}\ln {\frac{1+x}{1-x}}-\int \frac{x^{2}}{2} \frac{2}{ 1-x^{2}} dx$$

$$=\frac{x^{2}}{2}\ln {\frac{1+x}{1-x}}-\int \frac{-x^{2}+1-1}{1-x^{2}} dx$$

$$=\frac{x^{2}}{2}\ln {\frac{1+x}{1-x}}-\int dx-\int \frac{1}{1-x^{2}} dx$$

$$=\frac{x^{2}}{2}\ln {\frac{1+x}{1-x}+x-}\frac{1}{2}\ln {\frac{1+x}{1-x}+C}$$

$$=\frac{1}{2}\left( x^{2}+1\right) \ln \frac{1+x}{1-x}+x+C.$$

d)

$x^{3}$ u brojinku zapisujemo kao $x^{2}\cdot x$ , pa slijedi

$$\int \frac{x^{3}}{\sqrt{1+x^{2}}} dx =\int x^{2}\frac{x}{\sqrt{1+x^{2}}} dx$$

$$=\left\{ \begin{array}{cc} u=x^{2} & dv=\frac{x}{\sqrt{1+x^{2}}... ...rac{1}{2}\int \frac{2x}{\sqrt{1+x^{2}}} dx=\sqrt{1+x^{2}} \end{array} \right\}$$

$$=x^{2}\sqrt{1+x^{2}}-\int \sqrt{1+x^{2}}2x dx$$

$$=x^{2}\sqrt{1+x^{2}}-\int \sqrt{1+x^{2}} d\left( 1+x^{2}\right)$$

$$=x^{2}\sqrt{1+x^{2}}-\frac{2}{3}\left( x^{2}+1\right) ^{\frac{3}{2}}+C.$$

e)

Vrijedi

$$\int e^{x}\sin x dx =\left\{ \begin{array}{cc} u=e^{x} & dv=\sin x dx du=e^{x} dx & v=-\cos x \end{array} \right\}$$

$$=-e^{x}\cos x+\int e^{x}\cos x dx$$

$$=\left\{ \begin{array}{cc} u=e^{x} & dv=\cos x dx du=e^{x} dx & v=\sin x \end{array} \right\}$$

$$=-e^{x}\cos x+e^{x}\sin x-\int e^{x}\sin x dx.$$

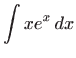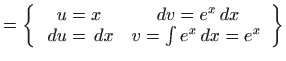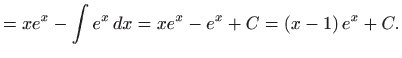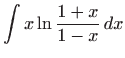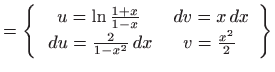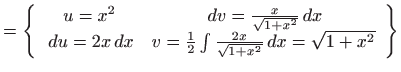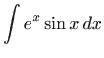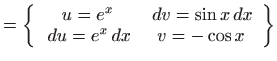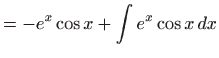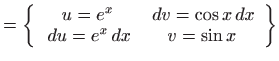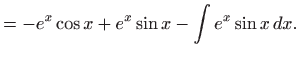Integral koji preostaje izračunati jednak je početnom integralu, označimo ga s $I$ , pa izjednačavanjem lijeve i desne strane dobivamo

$$I=e^{x}\cos x+e^{x}\sin x-I,$$

iz čega slijedi

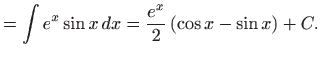$$2I =e^{x}\left( \cos x-\sin x\right)$$

$$I =\int e^{x}\sin x dx=\frac{e^{x}}{2}\left( \cos x-\sin x\right) +C.$$

Uvođenje novog argumenta     NEODREĐENI INTEGRAL     Rekurzivne formule