Izračunajte volumen tijela koje je omeđeno plohama
![]() ,
, ![]() ,
, ![]() ,
, ![]() i
i ![]() .
.
Rješenje.
Volumen tijela ![]() koje je omeđeno bazom
koje je omeđeno bazom ![]() u
u ![]() -ravnini i plohom
-ravnini i plohom ![]() , prema
, prema
![]() [M2, poglavlje 4.2.1], dan je s
[M2, poglavlje 4.2.1], dan je s
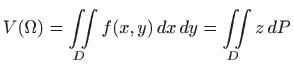 . . |
Na slici 4.7 je prikazano tijelo čiji volumen želimo izračunati i njegova projekcija na ![]() ravninu.
Budući da je tijelo odozgo omeđeno plohom
ravninu.
Budući da je tijelo odozgo omeđeno plohom
![]() , vrijedi
, vrijedi
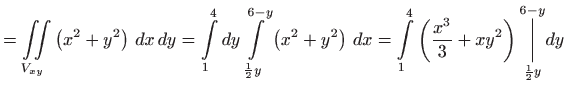 |
||
![$\displaystyle =\int\limits_{1}^{4}\left[ \frac{\left( 6-y\right) ^{3}}{3}+\left(
6-y\right) y^{2}-\frac{1}{3}\frac{y^{3}}{8}+\frac{1}{2}yy^{2}\right]
dy$](img1301.gif) |
||
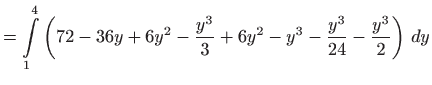 |
||
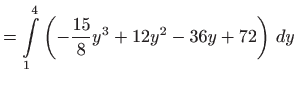 |
||
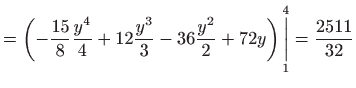 . . |