Odredite površinu onog dijela ravnine
![]() koji se nalazi u prvom oktantu projicirajući zadani dio
ravnine na
koji se nalazi u prvom oktantu projicirajući zadani dio
ravnine na ![]() - ravninu.
- ravninu.
Rješenje.
Površina dijela glatke plohe ![]() iznad
ograničenog područja
iznad
ograničenog područja ![]() u
u ![]() -ravnini dana je s
-ravnini dana je s
Ako želimo površinu računati preko projekcije na ![]() ravninu, samo u (4.3)
zamijenimo varijable
ravninu, samo u (4.3)
zamijenimo varijable ![]() i
i ![]() . Odnosno,
površina dijela glatke plohe
. Odnosno,
površina dijela glatke plohe ![]() iznad
ograničenog područja
iznad
ograničenog područja ![]() u
u ![]() -ravnini dana je s
-ravnini dana je s
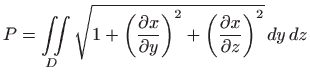 . . |
Odsječak ravnine
![]() u prvom oktantu i njegova projekcija na
u prvom oktantu i njegova projekcija na ![]() ravninu prikazani su na slici 4.9.
ravninu prikazani su na slici 4.9.
Zapišimo najprije
jednadžbu ravnine ![]() u obliku
u obliku ![]() :
:
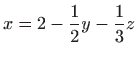 . . |
Vrijedi
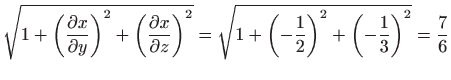 , , |
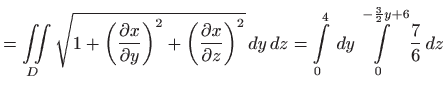 |
||
![$\displaystyle =\int\limits_{0}^{4} \frac{7}{6}z\underset{0}{\overset{-\frac{3}...
...imits_{0}^{4} \frac{7}{6}\left[ \left( -\frac{3}{2}
y+6\right) -0\right] dy$](img1334.gif) |
||
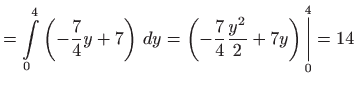 . . |