☰
matematika2
Površina dijela plohe u
VIŠESTRUKI INTEGRALI
Neposredna integracija u trostrukom
Područje integracije u trostrukom integralu
Postavite granice za integral
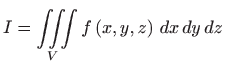 ako je područje V
ako je područje V
- a)
- kugla radijusa 2 sa središtem u ishodištu,
- b)
- unutrašnjost stošca
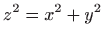 uz
uvjet
uz
uvjet
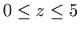 .
.
Rješenje.
- a)
- Jednadžba središnje sfere radijusa
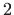 (slika 4.10) glasi
(slika 4.10) glasi
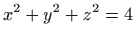 . . |
|
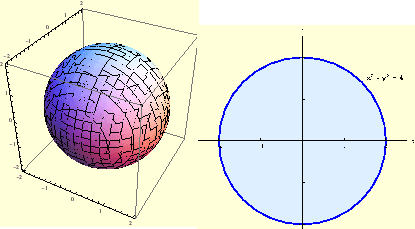
Slika:
Kugla radijusa 2 sa središtem u ishodištu, te njezina projekcija na 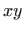 ravninu.
ravninu.
 |
Rub njene projekcije na 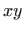 ravninu je kružnica s jednadžbom
ravninu je kružnica s jednadžbom
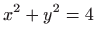 , , |
|
pa je područje integracije zadano s
i prema
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 4.3] vrijedi
[M2, poglavlje 4.3] vrijedi
- b)
- Projekcija stošca na
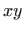 ravninu (slika 4.11) je krug
ravninu (slika 4.11) je krug
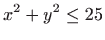 , , |
|
pa vrijedi
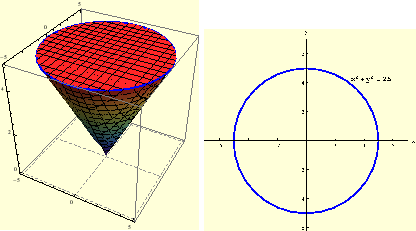
Slika:
Stožac određen sa
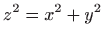 ,
,
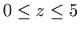 , i njegova projekcija na
, i njegova projekcija na 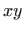 ravninu.
ravninu.
 |
Površina dijela plohe u
VIŠESTRUKI INTEGRALI
Neposredna integracija u trostrukom
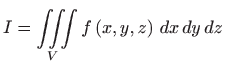 ako je područje V
ako je područje V
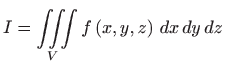 ako je područje V
ako je područje V
![]() ravninu je kružnica s jednadžbom
ravninu je kružnica s jednadžbom