Ispitajte je li
![]() opće rješenje diferencijalne jednadžbe
opće rješenje diferencijalne jednadžbe
![]() u području
u području ![]() i odredite
partikularno rješenje koje odgovara početnim uvjetima
i odredite
partikularno rješenje koje odgovara početnim uvjetima
![]() ,
,
![]() .
.
Rješenje.
Funkciju
![]() dva puta
deriviramo i dobivamo:
dva puta
deriviramo i dobivamo:
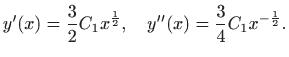
Uvrštavanjem derivacija u zadanu diferencijalnu jednadžbu slijedi
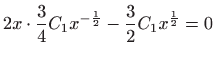 |
pa zaključujemo da je
![]() opće rješenje zadane
diferencijalne jednadžbe.
opće rješenje zadane
diferencijalne jednadžbe.
Da bismo odredili partikularno rješenje, u opće rješenje i njegovu prvu derivaciju
ćemo uvrstiti zadane početne uvjete. Na taj način iz uvjeta
![]() dobivamo
dobivamo ![]() , a potom, iz uvjeta
, a potom, iz uvjeta
![]() slijedi
slijedi ![]() .
Dakle, partikularno rješenje koje zadovoljava zadane početne uvjete glasi
.
Dakle, partikularno rješenje koje zadovoljava zadane početne uvjete glasi
![]() .
.