☰
matematika2
Bernoullijeva diferencijalna jednadžba
DIFERENCIJALNE JEDNADŽBE
Opće rješenje diferencijalne jednadžbe
Eulerova metoda
- a)
- Eulerovom metodom s korakom
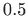 izračunajte
približne vrijednosti za
izračunajte
približne vrijednosti za
gdje je
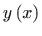 rješenje problema početnih vrijednosti
rješenje problema početnih vrijednosti
- b)
- Eulerovom metodom s korakom
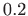 izračunajte
približnu vrijednost
izračunajte
približnu vrijednost
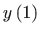 , ako je
, ako je
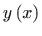 rješenje problema početnih vrijednosti
rješenje problema početnih vrijednosti
Rješenje.
- a)
- Vrijedi
Za korak
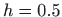 vrijedi
vrijedi
Formula za Eulerovu metodu
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.4] daje:
[M2, poglavlje 5.4] daje:
- b)
- Vrijedi
Za korak
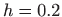 vrijedi
vrijedi
Koristeći formulu za Eulerovu metodu
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.4], dobivamo
[M2, poglavlje 5.4], dobivamo
Bernoullijeva diferencijalna jednadžba
DIFERENCIJALNE JEDNADŽBE
Opće rješenje diferencijalne jednadžbe