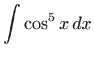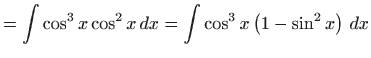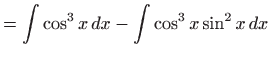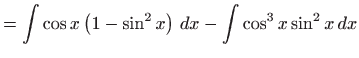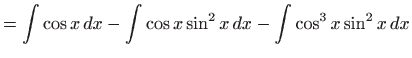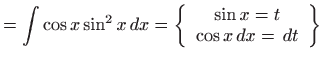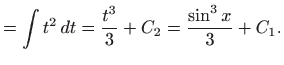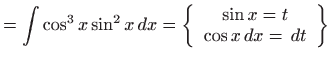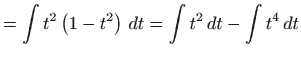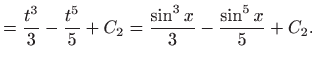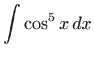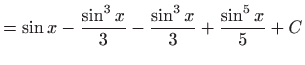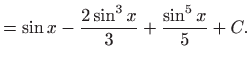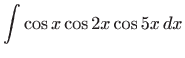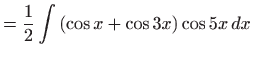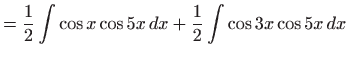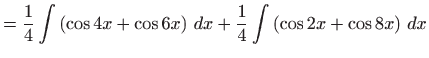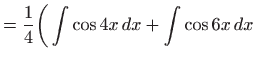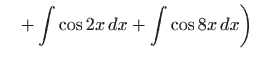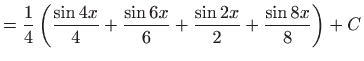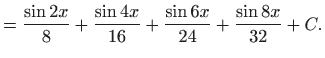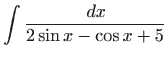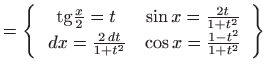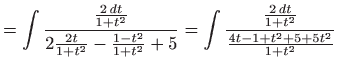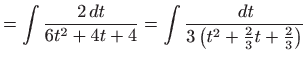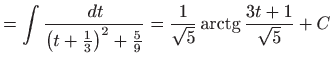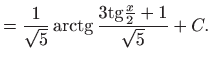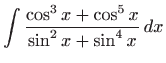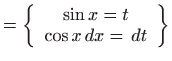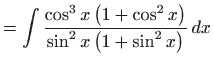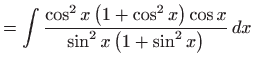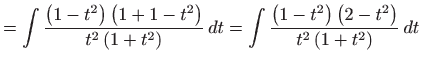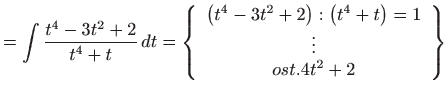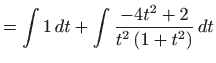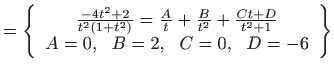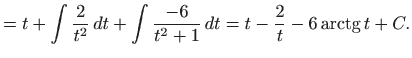☰
matematika2
Integriranje racionalnih funkcija
NEODREĐENI INTEGRAL
Integriranje iracionalnih funkcija racionalnom
Integriranje trigonometrijskih funkcija
Izračunajte integrale:
- a)
-
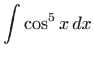 ,
,
- b)
-
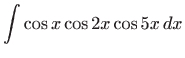 ,
,
- c)
-
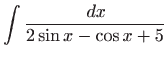 ,
,
- d)
-
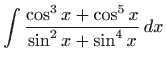 .
.
Rješenje.
- a)
- Vrijedi
Integrale označene sa 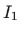 i
i 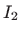 računamo posebno koristeći
jednostavne supstitucije.
računamo posebno koristeći
jednostavne supstitucije.
pa je konačno rješenje
- b)
- Podintegralnu funkciiju prvo raspišemo pomoću
trigonometrijskih formula pretvorbe, pa vrijedi
- c)
- Integral računamo koristeći univerzalnu trigonometrijsku
supstituciju
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 1.5.1].
[M2, poglavlje 1.5.1].
- d)
- Integrala računamo koristeći jednostavniju supstituciju:
Integriranje racionalnih funkcija
NEODREĐENI INTEGRAL
Integriranje iracionalnih funkcija racionalnom
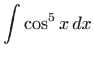 ,
,
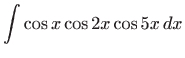 ,
,
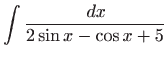 ,
,
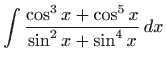 .
.
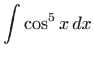 ,
,
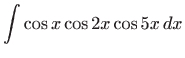 ,
,
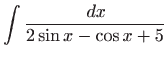 ,
,
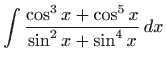 .
.