Odredite opće rješenje diferencijalne jednadžbe
![]() .
.
Rješenje.
U slučaju kada diferencijalna jednadžba ne sadrži eksplicitno nezavisnu varijablu ![]() tj. ima oblik
tj. ima oblik
![]() rješavamo ju uvođenjem supstitucije
rješavamo ju uvođenjem supstitucije
![]() . Tada je
. Tada je
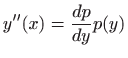 .
.
Nakon ovih zamjena zadana diferencijalna jednadžba poprima sljedeći oblik
![$\displaystyle p\left[2p-(y-1)\frac{dp}{dy}\right]=0.$](img2023.gif) |
Iz
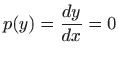 dobivamo partikularno rješenje diferencijalne jednadžbe
dobivamo partikularno rješenje diferencijalne jednadžbe
![]() .
.
Iz
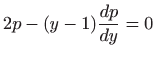 ćemo, separiranjem varijabli, doći do općeg rješenja zadane diferencijalne jednadžbe. Naime, vrijedi
ćemo, separiranjem varijabli, doći do općeg rješenja zadane diferencijalne jednadžbe. Naime, vrijedi
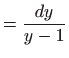 |
||
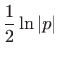 |
||
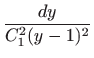 |
Nakon integriranja dobivamo opće rješenje oblika
![]() .
.