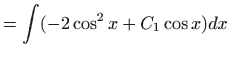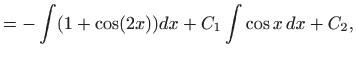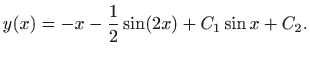☰
matematika2
Snižavanje reda diferencijalne jednadžbe,
DIFERENCIJALNE JEDNADŽBE
Snižavanje reda diferencijalne jednadžbe,
Snižavanje reda diferencijalne jednadžbe, 2. primjer
Odredite opće rješenje diferencijalne
jednadžbe
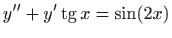 .
.
Rješenje.
Diferencijalnu jednadžbu oblika
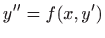 rješavamo svođenjem na diferencijalnu jednadžbu prvog reda pomoću supstitucije
rješavamo svođenjem na diferencijalnu jednadžbu prvog reda pomoću supstitucije
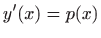 .
.
Uvrštavanje
u zadanu diferencijalnu jednadžbu daje
Ovo je linearna diferencijalna jednadžba prvog reda koju ćemo riješiti primjenom formule
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.8]. Vrijedi
[M2, poglavlje 5.8]. Vrijedi
Da bismo dobili opće rješenje zadane jednadžbe, pomoćnu funkciju 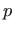 zamjenit
ćemo s
zamjenit
ćemo s
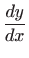 . Vrijedi
. Vrijedi
pa opće rješenje zadane jednadžbe glasi
Snižavanje reda diferencijalne jednadžbe,
DIFERENCIJALNE JEDNADŽBE
Snižavanje reda diferencijalne jednadžbe,
![]() .
.
![]() rješavamo svođenjem na diferencijalnu jednadžbu prvog reda pomoću supstitucije
rješavamo svođenjem na diferencijalnu jednadžbu prvog reda pomoću supstitucije
![]() .
.
![$\displaystyle = e^{-\int \mathop{\mathrm{tg}}\nolimits x dx}\left[\int \sin (2x)e^{\int\mathop{\mathrm{tg}}\nolimits x dx}dx+C_1\right]$](img2008.gif)
![$\displaystyle = e^{\ln \vert\cos x\vert}\left[\int 2\sin x\cos xe^{-\ln \vert\cos x\vert}dx+C_1\right]$](img2009.gif)
![$\displaystyle = \vert\cos x\vert\left[2sgn (\cos x)\int \sin x dx+C_1\right]$](img2010.gif)