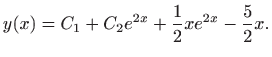Odredite opće rješenje diferencijalne jednadžbe
![]() .
.
Rješenje.
Ako je desna strana diferencijalne jednadžbe zbroj više funkcija
Pripadna homogena jednadžba zadane diferencijalne jednadžbe glasi
![]() , a njena karakteristična jednadžba
, a njena karakteristična jednadžba
![]() ima rješenja
ima rješenja
![]() i
i
![]() . Dakle, opće rješenje homogene jednadžbe je
. Dakle, opće rješenje homogene jednadžbe je
![]() .
.
Odredimo sada partikularno rješenje
![]() diferencijalne jednadžbe
diferencijalne jednadžbe
![]() . Iz (5.7) slijedi
. Iz (5.7) slijedi
![]() ,
, ![]() ,
, ![]() i
i ![]() pa je
pa je
![]() za neku konstantu
za neku konstantu ![]() .
Nakon uvrštavanja i sređivanja slijedi
.
Nakon uvrštavanja i sređivanja slijedi
![]() .
.
Prema (5.7), partikularno rješenje jednadžbe
![]() ima oblik
ima oblik
![]() (sada je
(sada je
![]() ,
, ![]() ,
, ![]() i
i ![]() ), a uvrštavanje daje
), a uvrštavanje daje
![]() .
.
Iz svega dobivenog zaključujemo da je opće rješenje zadane diferencijalne jednadžbe