☰
matematika2
Zadaci za vježbu
DIFERENCIJALNE JEDNADŽBE
METODA NAJMANJIH KVADRATA I
Rješenja zadataka za vježbu
- 1.
- Ne.
- 2.
-
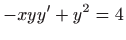 .
.
- 3.
-
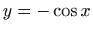 .
.
- 4.
- a)
-
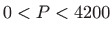 ,
,
- b)
-
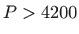 .
.
- 5.
-
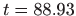 .
.
- 6.
- a)
-
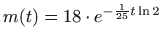 ,
,
- b)
-
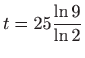 .
.
- 7.
-
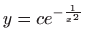 .
.
- 8.
-
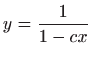 .
.
- 9.
-
![$ \displaystyle y=\ln \left[c(1+x^2)-1\right]$](img2357.gif) ,
, 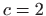 ,
,
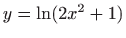 .
.
- 10.
- a)
-
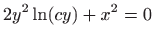 ,
,
- b)
-
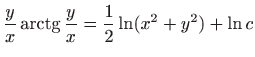 ,
,
- c)
-
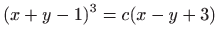 ,
,
- d)
-
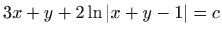 ,
,
- e)
-
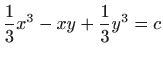 ,
,
- f)
-
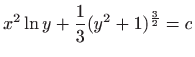 ,
,
- g)
-
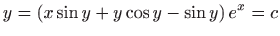 .
.
- 11.
-
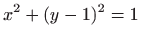 .
.
- 12.
-
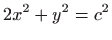 .
.
- 13.
-
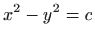 .
.
- 14.
-
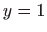 ,
, 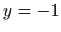 .
.
- 15.
-
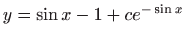 ,
, 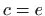 ,
,
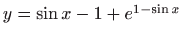 .
.
- 16.
-
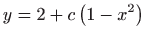 ,
, 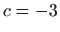 ,
,
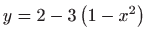 .
.
- 17.
- a)
-
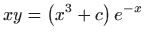 ,
,
- b)
-
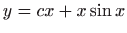 ,
,
- c)
-
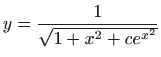 ,
,
- d)
-
![$ \displaystyle c=\frac{1}{\sqrt[3]{c\cos ^{3}x-3\sin x\cos
^{2}x}}$](img2381.gif) ,
,
- e)
-
![$ \displaystyle y=\frac{1}{x\sqrt[3]{3\ln \frac{c}{x}}}$](img2382.gif) .
.
- 18.
-
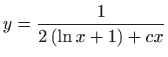 ,
, 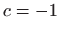 ,
,
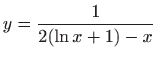 .
.
- 19.
-
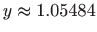 .
.
- 20.
-
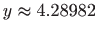 .
.
- 21.
- a)
-
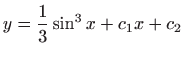 .
.
- b)
-
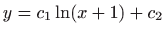 .
.
- c)
-
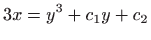 .
.
- d)
-
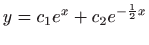 .
.
- e)
-
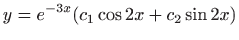 .
.
- 22.
-
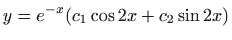 ,
,
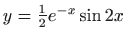 .
.
- 23.
- a)
-
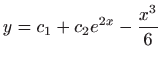 .
.
- b)
-
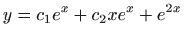 .
.
- c)
-
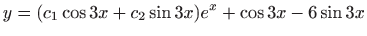 .
.
- d)
-
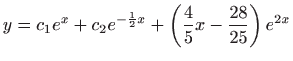 .
.
- 24.
-
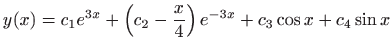 .
.
- 25.
-
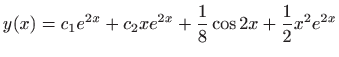 .
.
- 26.
-
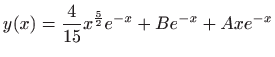 .
.
- 27.
-
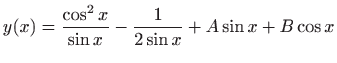 .
.
- 28.
-
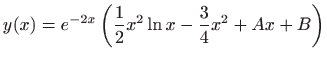 .
.
- 29.
-
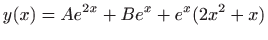 .
.
- 30.
-
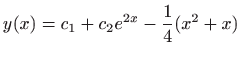 ,
,
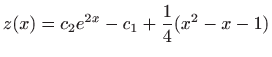 .
.
- 31.
-
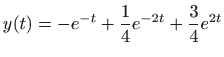 ,
,
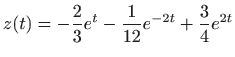 .
.
- 32.
-
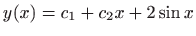 ,
,
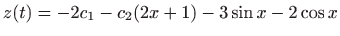 .
.
- 33.
- a)
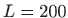 ,
, 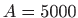 , b)
, b)
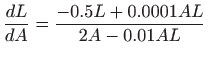 .
.
Zadaci za vježbu
DIFERENCIJALNE JEDNADŽBE
METODA NAJMANJIH KVADRATA I
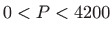 ,
,
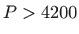 .
.
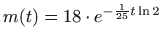 ,
,
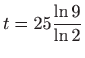 .
.
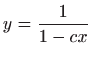 .
.
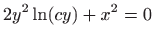 ,
,
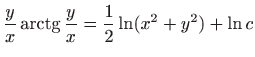 ,
,
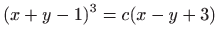 ,
,
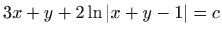 ,
,
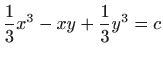 ,
,
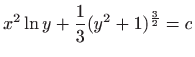 ,
,
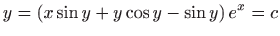 .
.
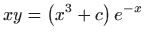 ,
,
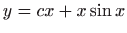 ,
,
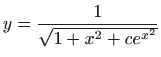 ,
,
![$ \displaystyle c=\frac{1}{\sqrt[3]{c\cos ^{3}x-3\sin x\cos
^{2}x}}$](img2381.gif) ,
,
![$ \displaystyle y=\frac{1}{x\sqrt[3]{3\ln \frac{c}{x}}}$](img2382.gif) .
.
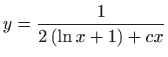 ,
, 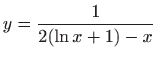 .
.
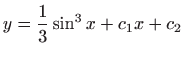 .
.
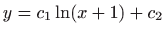 .
.
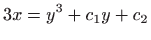 .
.
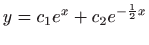 .
.
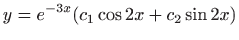 .
.
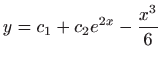 .
.
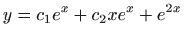 .
.
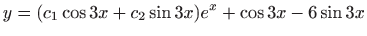 .
.
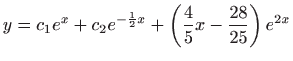 .
.
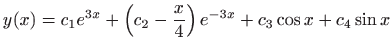 .
.
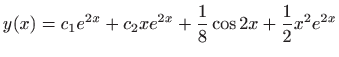 .
.
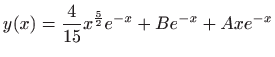 .
.
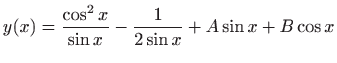 .
.
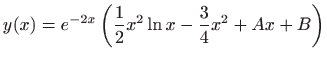 .
.
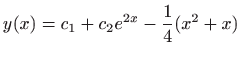 ,
,
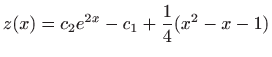 .
.
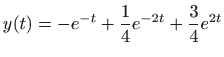 ,
,
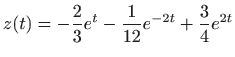 .
.
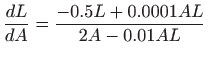 .
.