Ukoliko nisu sva mjerenja jednako pouzdana (ili jednako precizna), možemo im
pridružiti dijagonalnu matricu težina ![]() , čiji su svi dijagonalni elementi
pozitivni. Na taj način dobivamo
problem najmanjih kvadrata s težinama,
, čiji su svi dijagonalni elementi
pozitivni. Na taj način dobivamo
problem najmanjih kvadrata s težinama,
odnosno
Za rješevanje problema koriste se metode iz poglavlja 6.1.2 i 6.2.
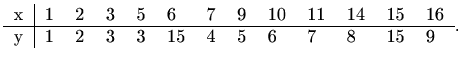
Točke
i regresijski pravac s težinama,
prikazani su na slici 6.4.