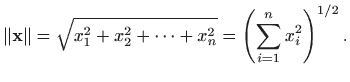×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 METODA NAJMANJIH KVADRATA I     METODA NAJMANJIH KVADRATA I     Linearna regresija

Problem najmanjih kvadrata

U ovom poglavlju dat ćemo kratki uvod u matrični problem najmanjih kvadrata. Metoda najmanjih kvadrata se koristi kod preodređenih sustava $Ax=b$ u slučaju kada imamo više jednadžbi nego nepoznanica i kada sustav nije rješiv po Kronecker-Capellijevom teoremu (vidi M1, teorem 2.5).

Problem najmanjih kvadrata se često koristi u raznim tehničkim primjenama te u ekonomiji (linearna regresija).

Duljina ili norma $n$ -dimenzionalnog vektora $\mathbf{x}=\begin{bmatrix}x_1 & x_2 & \cdots & x_n \end{bmatrix}^T$ je broj (vidi M1, poglavlje 3.6)

$$\Vert \mathbf{x}\Vert=\sqrt{x_1^2+x_2^2+\cdots + x_n^2} =\left(\sum_{i=1}^n x_i^2\right)^{1/2}.$$

Poglavlja

• Linearna regresija
• Metoda najmanjih kvadrata
• Problem najmanjih kvadrata s težinama