Postupak iz prethodnog poglavlja primjenjiv je i na višedimenzionalne
probleme. U ovom poglavlju pokazat ćemo da je postupak primjenjiv
uvijek kada matrica sustava ![]() ima linearno nezavisne stupce te je u
tom slučaju rješenje problema najmanjih kvadrata jedinstveno.
ima linearno nezavisne stupce te je u
tom slučaju rješenje problema najmanjih kvadrata jedinstveno.
Neka je zadan preodređeni sustav ![]() od
od ![]() jednadžbi s
jednadžbi s ![]() nepoznanica, pri čemu je
nepoznanica, pri čemu je ![]() . Kako za normu vektora
. Kako za normu vektora ![]() vrijedi
vrijedi
![]() , problem najmanjih kvadrata
, problem najmanjih kvadrata
možemo zapisati kao
Uvedimo oznaku
Ideju za postupak rješavanja daje nam jednodimenzionalni slučaj: ako su
U višedimenzionalnom slučaju tome odgovara
pa je
odnosno
Ova jednadžba zove se normalna jednadžba. Dokažimo sada da ovaj intuitivni postupak zaista daje rješenje.
a kako se radi o matricama dimenzije
Uvrštavanje u
Izraz
Dakle, uvijek je
odnosno vrijednost
Dokažimo sada da je rješenje
![]() jedinstveno. Ako je
jedinstveno. Ako je
onda je
Primijetimo da su vektori
![]() i
i
![]() međusobno okomiti:
međusobno okomiti:
Geometrijski to znači da je vektor
Rješenje problema najmanjih kvadrata
![]() zove se još i kvadratična
prilagodba
sustavu
zove se još i kvadratična
prilagodba
sustavu
![]() u smislu najmanjih kvadrata.
Kvalitetu prilagodbe mjerimo s
u smislu najmanjih kvadrata.
Kvalitetu prilagodbe mjerimo s
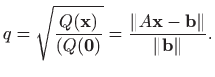
Iz činjenice da je
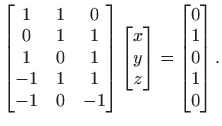
Normalna jednadžba glasi
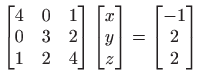
pa je rješenje dano s
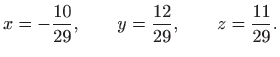
Kvaliteta prilagodbe je
Odgovarajući Matlab program glasi
Octave On-line[Octave On-line Home] [Octave User's Guide] |
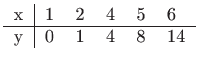
provucimo kvadratnu parabolu
koja ima najbolju kvadratičnu prilagodbu. Dakle, moramo naći koeficijente parabole tako da je
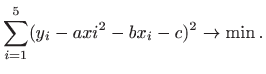
Ovaj problem možemo zapisati kao problem najmanjih kvadrata
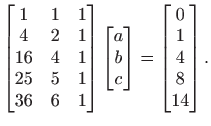
Rješavanje normalne jednadžbe daje
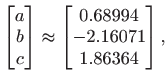
a kvaliteta prilagodbe iznosi
Parabola i slike mogu se dobiti sljedećim Matlab programom
Octave On-line[Octave On-line Home] [Octave User's Guide] |