×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Primjer     NEODREĐENI INTEGRAL     Univerzalna trigonometrijska supstitucija

Racionalne funkcije trigonometrijskih funkcija

Integrali ove klase funkcija su također uvijek elementarne funkcije. Ukratko, integral racionalne funkcije trigonometrijskih funkcija odgovarajućom se supstitucijom svede na integral racionalne funkcije koji se onda riješi postupkom opisanim u poglavlju 1.4.

Definicija 1.3   Neka su $f_1,\ldots,f_n$ elementarne funkcije. Racionalna funkcija od funkcija $f_1,\ldots,f_n$ je svaka funkcija $f$ koju dobijemo konačnim brojem zbrajanja, oduzimanja, množenja i dijeljenja funkcija $f_1,\ldots,f_n$ . Za funkciju $f$ koristimo oznake

$$f=\mathcal{R} (f_1,\ldots,f_n)\quad \textrm{ili}\quad f(x)=\mathcal{R} (f_1(x),\ldots,f_n(x)).$$

Integral oblika

$$\int \mathcal{R} (\sin x,\cos x) dx$$

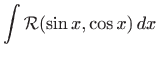
svodi se supstitucijom na integral racionalne funkcije. Primijetimo da u prethodnom izrazu nema potrebe navoditi funkcije $\mathop{\mathrm{tg}}\nolimits x$ i $\mathop{\mathrm{ctg}}\nolimits x$ jer su one već racionalne funkcije funkcija $\sin x$ i $\cos x$ . Za svođenje na integral racionalne funkcije koristimo univerzalnu trigonometrijsku supstituciju, a u nekim posebnim slučajevima možemo koristiti i neke jednostavnije supstitucije.

Poglavlja

• Univerzalna trigonometrijska supstitucija
• Jednostavnije supstitucije