Racionalnu funkciju je uvijek moguće integrirati, odnosno integral takve funkcije je uvijek elementarna funkcija. Postupak integriranja je složen i sastoji se od četiri koraka: eliminacija zajedničkih nul-točaka brojnika i nazivnika, svođenje na pravu racionalnu funkciju, rastavljanje na parcijalne razlomke i integriranje dobivenih izraza pomoću neposrednog integriranja, metode supstitucije ili metode parcijalne integracije. Integriranje racionalnih funkcija je važno jer se i integrali racionalnih funkcija trigonometrijskih funkcija (poglavlje 1.5), kao i integrali nekih iracionalnih funkcija (poglavlje 1.5), odgovarajućim transformacijama svode na integrale racionalnih funkcija.
Neka je zadana racionalna funkcija
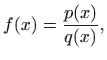
gdje su