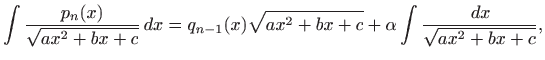 |
(1.7) |
Vrijedi formula
Integrali ovog tipa također se mogu rješavati
trigonometrijskim i
Eulerovim
supstitucijama. Međutim, ako je red polinoma ![]() velik,
onda trigonometrijske i Eulerove supstitucije vode na složeni
integral racionalne funkcije, pa je metoda neodređenih koeficijenata
jednostavnija.
velik,
onda trigonometrijske i Eulerove supstitucije vode na složeni
integral racionalne funkcije, pa je metoda neodređenih koeficijenata
jednostavnija.
 |
||
 |
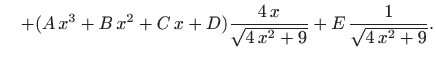 |
Izjednačavanje koeficijenata uz iste potencije od
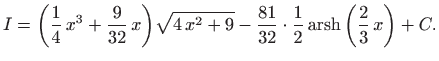
Izvedite za vježbu sve preskočene detalje.