×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Metoda neodređenih koeficijenata     Integriranje nekih iracionalnih funkcija     Integriranje reda funkcija

Binomni integral

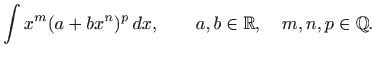
Binomni integral je integral oblika

$$\int x^m(a+bx^n)^p dx, \qquad a,b\in \mathbb{R}, \quad m,n,p\in \mathbb{Q}.$$

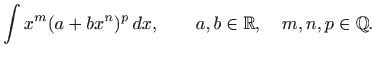
Vidimo da se u binomnom integralu mogu pojaviti i drugi korijeni osim kvadratnog, ali je zato oblik podintegralne funkcije nešto jednostavniji. Sljedeći teorem daje nam nužne i dovoljne uvjete rješivosti binomnog integrala.

Teorem 1.8   Binomni integral je elementarno rješiv ako i samo ako je jedan od brojeva

$$p,\qquad \frac{m+1}{n}, \qquad \frac{m+1}{n}+p$$

cijeli broj.

Dokaz.

Dokažimo dovoljnost. Vrijedi

$$\int x^m(a+bx^n)^p dx = \left\{\begin{aligned}x^n&=t,\quad x =t^{1/n}, dx&=\frac{1}{n} t^{\frac{1}{n}-1} dt \end{aligned}\right\}$$

$$= \frac{1}{n} \int t^{\frac{m}{n}} (a+bt)^p t^{\frac{1}{n}-1} dt$$

$$= \frac{1}{n} \int \bigg(\frac{a+bt}{t}\bigg)^p t^{\frac{m+1}{n}+p-1} dt.$$

Razlikujemo tri slučaja:

i.

ako je $p\in \mathbb{Z}$ , onda koristimo supstituciju $t=z^k$ , gdje je $k$ najmanji nazivnik nakon kraćenja od $(m+1)/n$ ,

ii.

ako je $(m+1)/n$ cijeli broj, onda koristimo supstituciju $a+bt=z^k$ , gdje je $k$ nazivnik od $p$ , a

iii.

ako je $(m+1)/n+p$ cijeli broj, onda koristimo supstituciju $(a+bt)/t=z^k$ , gdje je $k$ nazivnik od $p$ .

Svaka od tri navedene supstitucije vodi na integral racionalne funkcije koji se rješava pomoću postupaka iz poglavlja 1.4. S ovim smo dokazali dovoljnost.

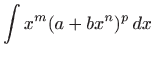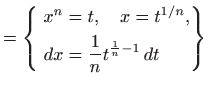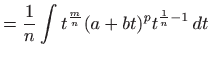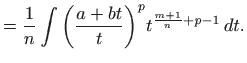Dokaz nužnosti, odnosno dokaz da binomni integral nije elementarno rješiv kada nisu ispunjeni slučajevi i.-iii. je složen pa ga izostavljamo.     

Q.E.D.

Primjer 1.13   Kod rješavanja integrala

$$I= \int \sqrt[3]{3x-x^3} dx$$

treba prvo prepoznati da se radi o binomnom integralu. Zaista, iz oblika

$$I=\int \sqrt[3]{x(3-x^2)} dx=\int x^{\frac{1}{3}}(3-x^2)^{\frac{1}{3}} dx$$

zaključujemo da se radi o binomnom integralu uz $m=1/3$ , $n=2$ i $p=1/3$ . Vrijedi

$$p\notin \mathbb{Z}, \qquad \frac{m+1}{n}=\frac{2}{3} \notin \mathbb{Z},\qquad \frac{m+1}{n}+p=1 \in \mathbb{Z},$$

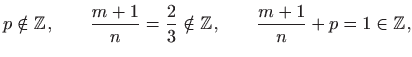
pa je integral elementarno rješiv po teoremu 1.8. Integral rješavamo postupkom danim u dokazu teorema 1.8:

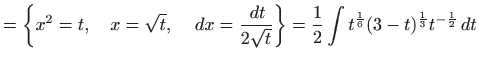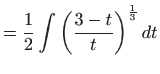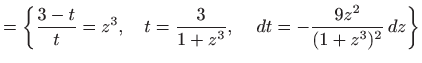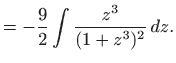$$I =\bigg\{ x^2=t,\quad x =\sqrt{t},\quad dx=\frac{ dt}{2\sqrt{... ...bigg\}=\frac{1}{2}\int t^{\frac{1}{6}}(3-t)^{\frac{1}{3}} t^{-\frac{1}{2}} dt$$

$$=\frac{1}{2}\int \bigg( \frac{3-t}{t}\bigg)^{\frac{1}{3}} dt$$

$$= \bigg\{ \frac{3-t}{t}=z^3, \quad t=\frac{3}{1+z^3}, \quad dt=-\frac{9z^2}{(1+z^3)^2} dz \bigg\}$$

$$= -\frac{9}{2} \int \frac{z^3}{(1+z^3)^2} dz.$$

Za vježbu riješite integral do kraja.

Zadatak 1.9   Izračunajte integrale:

$$\int x^{-11}(1+x^4)^{-1/2} dx,$$

$$\int \frac{\sqrt{1+\sqrt[3]{x}}}{\sqrt[3]{x^2}} dx.$$

Metoda neodređenih koeficijenata     Integriranje nekih iracionalnih funkcija     Integriranje reda funkcija