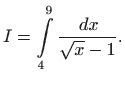
Određeni integral možemo riješiti tako da prvo riješimo pripadni neodređeni integral, a potom uvrstimo granice prema Newton-Leibnitzovoj formuli. Promotrimo integral
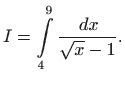
Prvo pomoću supstitucije riješimo neodređeni integral:
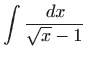 |
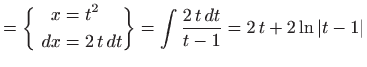 |
|
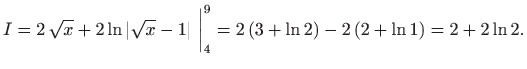
Prilikom zamjene varijabli možemo izvršiti i odgovarajuću zamjenu granica. U tom slučaju određeni integral rješavamo na sljedeći način:
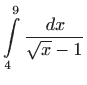 |
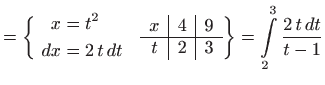 |
|
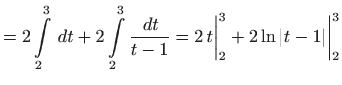 |
||
Kod zamjene granica trebamo uvijek paziti da ona bude dobro
definirana. Tako u ovom primjeru supstitucija ![]() zapravo znači
zapravo znači
![]() , pa smo prema tome i odabrali nove granice.
Posebno oprezan treba biti kod zamjene granica u slučaju periodičkih
(trigonometrijskih) funkcija.
, pa smo prema tome i odabrali nove granice.
Posebno oprezan treba biti kod zamjene granica u slučaju periodičkih
(trigonometrijskih) funkcija.
Formula za parcijalnu integraciju također vrijedi u određenom integralu:
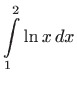 |
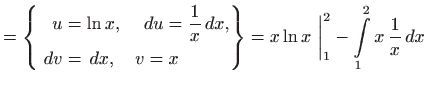 |
|
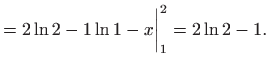 |