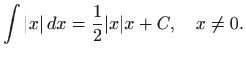Kao što smo već kazali, tablicu osnovnih integrala dobijemo
čitajući tablicu osnovnih derivacija
(vidi
![]() M1, poglavlje 5.1.5)
zdesna na lijevo, uz odgovarajuće manje prilagodbe. Sljedeće formule vrijede
za
M1, poglavlje 5.1.5)
zdesna na lijevo, uz odgovarajuće manje prilagodbe. Sljedeće formule vrijede
za
![]() , ukoliko nije drukčije navedeno.
Za konstantnu funkciju i potencije vrijedi:
, ukoliko nije drukčije navedeno.
Za konstantnu funkciju i potencije vrijedi:
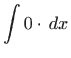 |
||
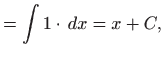 |
||
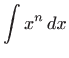 |
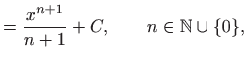 |
|
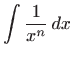 |
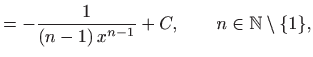 |
|
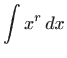 |
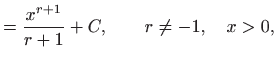 |
|
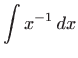 |
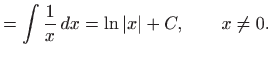 |
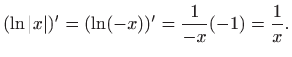
Za eksponencijalne funkcije imamo
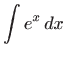 |
||
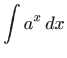 |
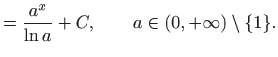 |
 |
||
 |
||
 |
||
 |
 |
||
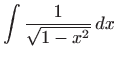 |
Primijetimo da integrali funkcija
Konačno, formule za derivacije hiperbolnih funkcija povlače
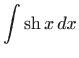 |
||
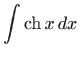 |
||
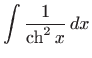 |
||
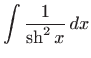 |
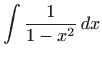 |
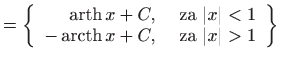 |
|
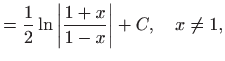 |
||
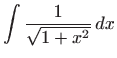 |
||
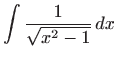 |
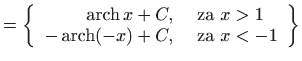 |
|
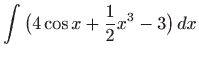 |
 |
|
 |
 |
 |
|
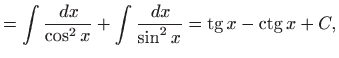 |
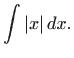
Kada je
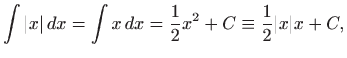
a kada je
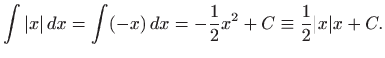
Dakle,