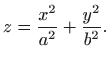 |
Opća formula eliptičkog paraboloida glasi
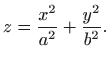 |
Nivo-krivulje eliptičkog paraboloida su elipse,
a presjeci s ravninama koje su paralelne s
![]() -ravninom i
-ravninom i ![]() ravninom su parabole (vidi sliku
3.14).
ravninom su parabole (vidi sliku
3.14).
Paraboloid na slici možemo prikazati i parametarski kao skup
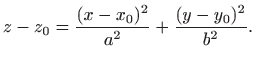 |
Zamjenom varijabli dobijemo eliptički paraboloid uzduž neke
druge osi, a predznak nezavisne varijable određuje na
koju stranu je paraboloid otvoren.
Na slici 3.16 prikazan je paraboloid
![]() .
.