Ploha drugog reda je skup svih točaka trodimenzionalnog prostora koje zadovoljavaju jednadžbu drugog stupnja (ili reda):
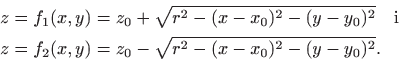 |
Nadalje,
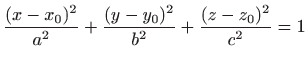 |
Nivo-krivulje elipsoida kao i presjeci s ravninama paralelnim s ![]() - i
- i
![]() -ravninama su elipse.
-ravninama su elipse.
Elipsoid na slici možemo definirati i parametarski kao skup točaka: