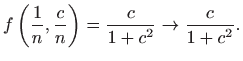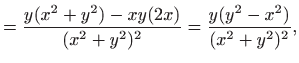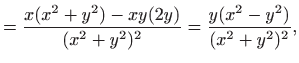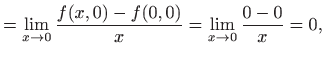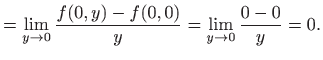Definicija 3.7 Parcijalna derivacija
funkcije
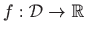 ,
,
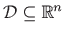 , po varijabli
, po varijabli
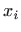 u točki
u točki
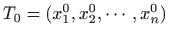 je derivacija funkcije
jedne varijable
je derivacija funkcije
jedne varijable
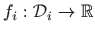 ,
,
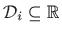 , definirane s
, definirane s
u točki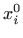 .
Dakle,
.
Dakle,
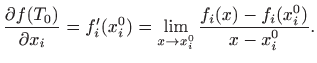
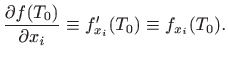
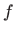 u točki
u točki 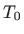 postoje parcijalne derivacije
postoje parcijalne derivacije
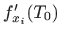 po svim varijablama
po svim varijablama
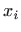 , onda kažemo da je funkcija
, onda kažemo da je funkcija 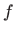 derivabilna u točki
derivabilna u točki
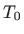 . Ako je
funkcija
. Ako je
funkcija 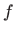 derivabilna u svakoj točki
derivabilna u svakoj točki
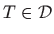 , onda kažemo da je
, onda kažemo da je
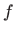 derivabilna funkcija.
derivabilna funkcija.
u točki
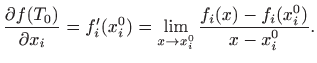
Za parcijalne derivacije još koristimo i sljedeće oznake:
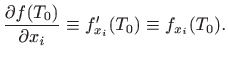
Ako za funkciju
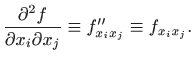
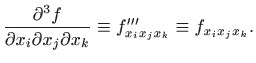
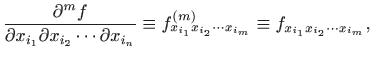
![\begin{equation*}
\begin{aligned}
f'_x(x,y) &=\frac{\partial[\sin(x+y^2)]}{\part...
...{\partial[\sin(x+y^2)]}{\partial y}=2y\cos(x+y^2).
\end{aligned}\end{equation*}](img1432.gif)
![\begin{equation*}
\begin{aligned}
f''_{xx}(x,y)
&=\frac{\partial\left[f'_x(x,y)\...
...(x+y^2)]}{\partial y}=2\cos(x+y^2)-4y^2\sin(x+y^2).
\end{aligned}\end{equation*}](img1433.gif)
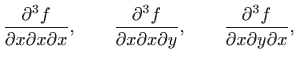
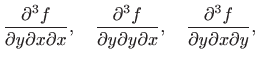
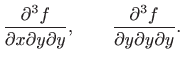
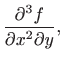
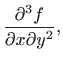
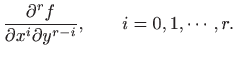
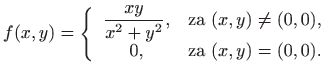
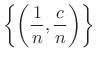 konvergiraju prema točki
konvergiraju prema točki