×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Nepravi integral     VIŠESTRUKI INTEGRALI     Cilindrične i sferne koordinate

Trostruki integral

Trostruki integral neprekidne funkcije $f:D\to \mathbb{R}$ , $D\subseteq \mathbb{R}^3$ , računamo slično kao i dvostruki integral. Ako je područje integracije kvadar,

$$D=[a,b]\times [c,d]\times [e,g],$$

onda je

$$\iiint\limits_D f(x,y,z) dx dy dz= \int\limits _a^b \bigg[ \int\limits _c^d \bigg( \int\limits _e^g f(x,y,z) dz\bigg) dy\bigg] dx,$$

pri čemu je $dV=dx dy dz$ element volumena. Kao i u slučaju dvostrukog integrala, mogući su i drugi redoslijedi integriranja.

Ako je područje $D$ određeno relacijama

$$a \leq x\leq b,$$

$$h_1(x) \leq y\leq h_2(x),$$

$$g_1(x,y) \leq z\leq g_2(x,y),$$

onda je

$$\iiint\limits_D f(x,y,z) dV = \int\limits _a^b \bigg[ \int\limit... ...\bigg( \int\limits _{g_1(x,y)}^{g_2(x,y)} f(x,y,z) dz\bigg) dy\bigg] dx.$$

Tipične primjene trostrukog integrala su sljedeće:

• ako je $f(x,y,z)$ gustoća tijela koje zaprema područje $D$ u točki $T=(x,y,z)$ , onda je trostruki integral $\iiint_D f(x,y,z) dV$ jednak masi tog tijela;
• ako je $f(x,y,z)=1$ , onda trostruki integral daje volumen područja^4.4 $D$ ,
  $$V(D)=\iiint\limits_D dV = \int\limits _a^b \int\limits _{h_1(x)}^{h_2(x)} \int\limits _{g_1(x,y)}^{g_2(x,y)} dz dy dx.$$

Primjer 4.6   Odredimo volumen tijela omeđenog plohama $z=x^2+y^2$ i $z=\sqrt{x^2+y^2}$ . Radi se o volumenu područja između paraboloida i stošca čiji je presjek s ravninom $y=0$ prikazan na slici 4.8.

Slika: Projekcija presjeka paraboloida i stošca na $xz$ -ravninu

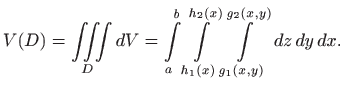
Za postavljanje integrala trebamo opisati područje $D$ . Nađimo presjek zadanih ploha: izjednačavanje $z=z$ daje jednadžbu

$$x^2+y^2=\sqrt{x^2+y^2}$$

koja ima rješenja $x=y=0$ i $\sqrt{x^2+y^2}=1$ , odnosno, $x^2+y^2=1$ . Dakle, prvo rješenje je ishodište gdje se dvije zadane plohe očito sijeku, a iz drugog rješenja vidimo da se plohe još sijeku u jediničnoj središnjoj kružnici za $z=1$ . Stoga je zadani volumen jednak

$$V=\int\limits _{-1}^1 \int\limits _{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int\limits _{x^2+y^2}^{\sqrt{x^2+y^2}} dz dy dx.$$

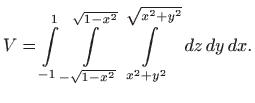
Integral ćemo izračunati koristeći cilindrične koordinate u sljedećem poglavlju.

Poglavlja

• Cilindrične i sferne koordinate

Nepravi integral     VIŠESTRUKI INTEGRALI     Cilindrične i sferne koordinate