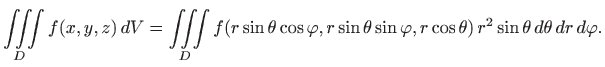Cilindrične i sferne koordinate

☰ matematika2

Trostruki integral Trostruki integral Zamjena varijabla

Cilindrične i sferne koordinate

Cilindrični koordinatni sustav odnosno cilindrične koordinate zadane su transformacijama:

$\displaystyle x$	$\displaystyle =r\cos \varphi ,$
$\displaystyle y$	$\displaystyle =r\sin \varphi ,$
$\displaystyle z$	$\displaystyle =z,$

pri čemu je $r\geq 0$ i $\varphi \in[0,2\pi]$ ili $\varphi \in[-\pi,\pi]$ . Dakle, element volumena jednak je umnošku površine baze i visine, s time što se površina baze računa u polarnim koordinatama (vidi sliku 4.9)

$\displaystyle dV=r dr d\varphi dz$

pa je

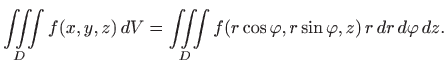
$\displaystyle \iiint\limits_D f(x,y,z) dV = \iiint\limits_D f(r\cos \varphi ,r\sin \varphi ,z) r dr d\varphi dz.$

**Slika:** Element volumena u cilindričnim koordinatama
$\begin{figure}\begin{center} \epsfig{file=slike/cilk.eps,width=6.0cm} \end{center}\end{figure}$

Primjer 4.7 Volumen iz primjera 4.6 lako je izračunati prelaskom na cilindrične koordinate. Vrijedi

$\displaystyle V$	$\displaystyle =\int\limits _0^{2\pi} \int\limits _0^1 \int\limits _{r^2}^r d... ...\vert _0^{2\pi} \cdot \int\limits _0^1 \big( z\big\vert _{r^2}^r\big) r dr$
	$\displaystyle = 2\pi \int\limits _0^1 (r^2-r^3) dr= \frac{1}{6} \pi.$

Sferne koordinate ili prostorne polarne koordinate zadane su transformacijama

$\displaystyle x$	$\displaystyle =r\sin\theta \cos \varphi ,$
$\displaystyle y$	$\displaystyle =r\sin\theta \sin \varphi ,$
$\displaystyle z$	$\displaystyle =r\cos \theta,$

pri čemu je $r\geq 0$ , a obično se odabire $\theta\in[0,\pi]$ i $\varphi \in[-\pi,\pi]$ . Uz oznaku $\rho=r\sin\theta$ možemo pisati

$\displaystyle x$	$\displaystyle =\rho \cos \varphi ,$
$\displaystyle y$	$\displaystyle =\rho \sin \varphi ,$
$\displaystyle z$	$\displaystyle =r\cos \theta.$

Sferne koordinate prikazane su na slici 4.10.

**Slika 4.10:** Sferne koordinate
$\begin{figure}\begin{center} \epsfig{file=slike/sfk.eps,width=7.2cm} \end{center}\end{figure}$

Zadatak 4.1 Prethodne formule služe za prebacivanje iz sfernih u Kartezijeve koordinate, $(r,\theta,\varphi )\to(x,y,z)$ . Izvedite formule za prebacivanje iz Kartezijevih u sferne koordinate, $(x,y,z)\to (r,\theta,\varphi )$ .

Primjer 4.8 Primjer jedne verzije sfernog koordinatnog sustava koji je često u upotrebi su zemljopisne karte. Udaljenost

se prikazuje kao nadmorska visina, kut $\varphi$ je zemljopisna dužina koja se mjeri istočno i zapadno od Greenwicha, što odgovara odabiru $\varphi \in[-\pi,\pi]$ , a kut $\theta$ je zemljopisna širina koja se mjeri sjeverno i južno od ekvatora, što odgovara odabiru $\theta\in[-\pi/2,\pi/2]$ . Odabir $\theta\in[0,\pi]$ je matematički povoljniji (vidi kasnije), jer je tada $\sin\theta\geq 0$ .

Za računanje trostrukog integrala u sfernom koordinatnom sustavu potrebno je izračunati element volumena . Iz slike 4.11 vidimo da je

$\displaystyle dV\approx a b dr,$

pri čemu je

$\displaystyle a=r\sin\theta d\varphi ,\qquad b=r d\theta.$

Dakle,

$\displaystyle dV\approx r^2\sin\theta d\theta dr d\varphi .$

Točan izraz za

sadrži još i druge članove, no oni teže nuli brže nego glavni izraz pa ih izostavljamo^4.5. Dakle, u sfernim koordinatama vrijedi

$\displaystyle \iiint\limits_D f(x,y,z) dV = \iiint\limits_D f(r\sin\theta \c... ...eta \sin \varphi , r\cos \theta) r^2\sin\theta d\theta dr d\varphi .$

**Slika 4.11:** Element volumena u sfernim koordinatama
$\begin{figure}\begin{center} \epsfig{file=slike/sfk1.eps,width=8.0cm} \end{center}\end{figure}$

Primjer 4.9 Volumen kugle

radijusa

jednak je

$\displaystyle V$	$\displaystyle = \iiint\limits_K 1\cdot dV = \int\limits _{-\pi}^{\pi} \int\limits _0^{\pi} \int\limits _0^R r^2\sin\theta dr d\theta d\varphi$
	$\displaystyle = \int\limits _{-\pi}^{\pi} d\varphi \cdot \int\limits _0^{\pi... ...\pi} \cdot (-\cos\theta)\bigg\vert _0^{\pi} \cdot \frac{r^3}{3} \bigg\vert _0^R$
	$\displaystyle =\frac{4}{3} R^3 \pi.$

Trostruki integral Trostruki integral Zamjena varijabla