| (5.8) |
Linearna diferencijalna jednadžba prvog reda ima oblik
Ako je ![]() , jednadžba je
homogena
, jednadžba je
homogena
Ovo je jednadžba sa separiranim varijablama:
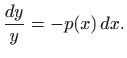
Dakle,
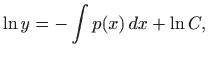
odnosno, rješenje homogene jednadžbe glasi
U nehomogenom slučaju jednadžba (5.8) je ekvivalentna s
Iz
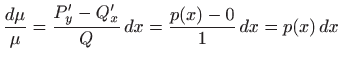
zaključujemo da je integrirajući faktor dan s
Množenjem jednadžbe (5.8) integrirajućim faktorom imamo
Formula za deriviranje produkta daje
![$\displaystyle \left[e^{\int p(x) dx} y\right]'=e^{\int p(x) dx} q(x),
$](img3012.gif)
a integriranje daje
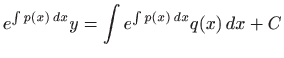
i formula (5.9) je dokazana.
Ako je ![]() , radi se o linearnoj diferencijalnoj jednadžbi prvog reda
oblika (5.8). Ako je
, radi se o linearnoj diferencijalnoj jednadžbi prvog reda
oblika (5.8). Ako je ![]() , onda imamo homogenu
jednadžbu
, onda imamo homogenu
jednadžbu
![]() . U ostalim slučajevima koristimo
supstituciju
. U ostalim slučajevima koristimo
supstituciju ![]() . Uvrštavanjem
. Uvrštavanjem
![$\displaystyle y'=\left[w^{\frac{1}{1-r}}\right]' = \frac{1}{1-r} w^{\frac{1}{1-r}-1} w'
= \frac{1}{1-r} w^{\frac{r}{1-r}} w'
$](img3031.gif)
dobili smo linearnu diferencijalnu jednadžbu prvog reda
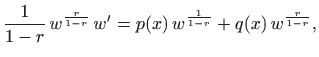
odnosno