Linearna diferencijalna jednadžba drugog reda glasi
pri čemu su funkcije
Pripadna homogena jednadžba glasi
U općenitom slučaju kada su ![]() i
i ![]() proizvoljne funkcije od
proizvoljne funkcije od ![]() ,
ne postoji univerzalna metoda za rješavanje linearne diferencijalne jednadžbe drugog reda
(5.14). No, takva metoda postoji u slučaju kada su
,
ne postoji univerzalna metoda za rješavanje linearne diferencijalne jednadžbe drugog reda
(5.14). No, takva metoda postoji u slučaju kada su ![]() i
i ![]() konstante (vidi poglavlje 5.9.3).
konstante (vidi poglavlje 5.9.3).
Poglavlje je organizirano na sljedeći način: prvo je uveden pojam linearne nezavisnosti funkcija. Potom je opisana struktura rješenja homogene jednadžbe (5.11). Nakon toga opisane su metode varijacije konstanti i metoda neodređenih koeficijenata za rješavanje nehomogene jednadžbe (5.14). Na kraju je opisan postupak rješavanja jednadžbe s konstantnim koeficijentima.
Ova definicija je formalno jednaka definiciji linearne nezavisnosti vektora
(vidi
![]() M1, poglavlje 2.5). Provjera linearne nezavisnosti je nešto
složenija i za nju su nam potrebni sljedeća definicija i teorem.
M1, poglavlje 2.5). Provjera linearne nezavisnosti je nešto
složenija i za nju su nam potrebni sljedeća definicija i teorem.
pri čemu je, na primjer,
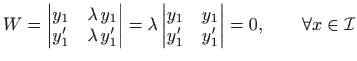
i teorem je dokazan.
Zaključujemo da su dvije funkcije linearno nezavisne čim je Wronskijan u barem jednoj točki različit od nule, što nije teško provjeriti.