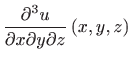 .
.
Za funkciju
![]() odredite
odredite
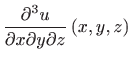 .
.
Rješenje.
Prema Teoremu
![]() [M2, teorem 3.3] vrijednost tražene derivacije ne ovisi o redoslijedu deriviranja po pojedinim varijablama pa redoslijed deriviranja biramo proizvoljno. Ovdje ćemo funkciju
[M2, teorem 3.3] vrijednost tražene derivacije ne ovisi o redoslijedu deriviranja po pojedinim varijablama pa redoslijed deriviranja biramo proizvoljno. Ovdje ćemo funkciju
![]() derivirati najprije po varijabli
derivirati najprije po varijabli
![]() . Vrijedi
. Vrijedi
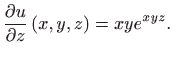 |
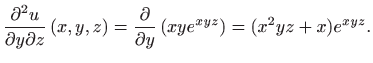 |
![$\displaystyle \frac{\partial ^3u}{\partial x\partial y\partial z}\left( x,y,z\r...
...\left[ \left(x^2yz+x\right)e^{xyz}\right]=\left(x^2y^2z^2+3xyz+1\right)e^{xyz}.$](img746.gif) |