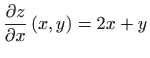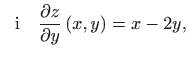☰
matematika2
Parcijalna diferencijalna jednadžba
FUNKCIJE VIŠE VARIJABLA
Totalni diferencijal drugog reda
Totalni diferencijal prvog reda
Odredite totalni diferencijal prvog reda funkcije
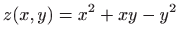 .
.
Rješenje.
Prema definiciji
![[*]](../icons.gif/crossref.gif) [M2, definicija 3.9] totalni diferencijal prvog reda za funkciju dviju varijabli
[M2, definicija 3.9] totalni diferencijal prvog reda za funkciju dviju varijabli
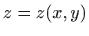 izračunavamo
po formuli
izračunavamo
po formuli
Budući da je
dobivamo da je totalni diferencijal prvog reda zadane funkcije
![]() .
.
![]() [M2, definicija 3.9] totalni diferencijal prvog reda za funkciju dviju varijabli
[M2, definicija 3.9] totalni diferencijal prvog reda za funkciju dviju varijabli
![]() izračunavamo
po formuli
izračunavamo
po formuli