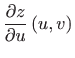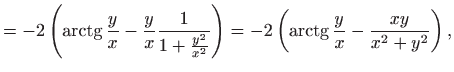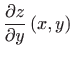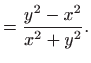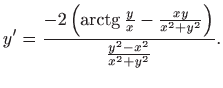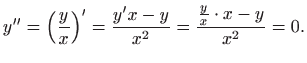☰
matematika2
Parcijalne derivacije složene funkcije
FUNKCIJE VIŠE VARIJABLA
Parcijalne derivacije funkcije dviju
Derivacija funkcije jedne varijable zadane implicitno
Odredite derivaciju prvog i drugog reda funkcije
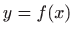 zadane implicitno sa
zadane implicitno sa
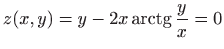 .
.
Rješenje.
Deriviranjem jednakosti
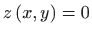 po varijabli
po varijabli 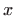 dobivamo
dobivamo
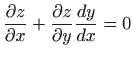 , , |
|
iz čega slijedi
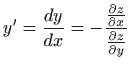 . . |
|
Izračunajmo najprije parcijalne derivacije funkcije 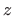 po varijablama
po varijablama 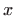 i
i 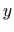 .
Vrijedi
.
Vrijedi
Sada je
Iz jednakosti
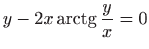 slijedi
slijedi
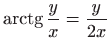 . Uz tu zamjenu, sređivanjem izraza za
. Uz tu zamjenu, sređivanjem izraza za
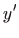 dobivamo
dobivamo
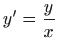 .
Za drugu derivaciju funkcije
.
Za drugu derivaciju funkcije
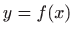 vrijedi
vrijedi
Parcijalne derivacije složene funkcije
FUNKCIJE VIŠE VARIJABLA
Parcijalne derivacije funkcije dviju
![]() zadane implicitno sa
zadane implicitno sa
![]() .
.
![]() po varijabli
po varijabli ![]() dobivamo
dobivamo
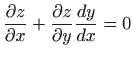 ,
,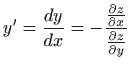 .
.![]() po varijablama
po varijablama ![]() i
i ![]() .
Vrijedi
.
Vrijedi