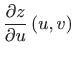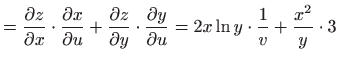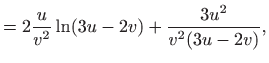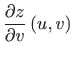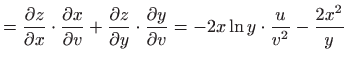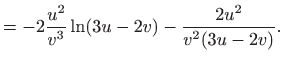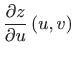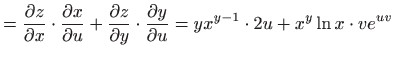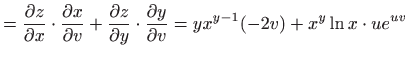☰ matematika2

Derivacija složene funkcije jedne FUNKCIJE VIŠE VARIJABLA Derivacija funkcije jedne varijable

Parcijalne derivacije složene funkcije dviju varijabli

Odredite parcijalne derivacije 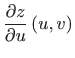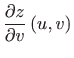$\displaystyle \frac{\partial z}{\partial u}\left( u,v\right)$ , $\displaystyle \frac{\partial z}{\partial v}\left( u,v\right)$ ako je:

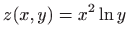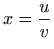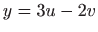a): $\displaystyle z(x,y)=x^2\ln y$ , $\displaystyle x=\frac{u}{v}$ , $\displaystyle y=3u-2v$ ;
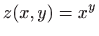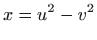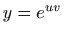b): $\displaystyle z(x,y)=x^y$ , $\displaystyle x=u^2-v^2$ , $\displaystyle y=e^{uv}$ .

Rješenje.

Primjenom [M2, teorem 3.5] slijedi:

a)

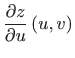$\displaystyle \frac{\partial z}{\partial u} \left( u,v\right)$	$\displaystyle = \frac{\partial z}{\partial x}\cdot \frac{\partial x}{\partial u... ...dot \frac{\partial y}{\partial u}=2x\ln y\cdot \frac{1}{v}+\frac{x^2}{y}\cdot 3$
	$\displaystyle =2\frac{u}{v^2}\ln (3u-2v)+\frac{3u^2}{v^2(3u-2v)},$
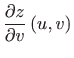$\displaystyle \frac{\partial z}{\partial v} \left( u,v\right)$	$\displaystyle = \frac{\partial z}{\partial x}\cdot \frac{\partial x}{\partial v... ...}\cdot \frac{\partial y}{\partial v}=-2x\ln y\cdot \frac{u}{v^2}-\frac{2x^2}{y}$
	$\displaystyle =-2\frac{u^2}{v^3}\ln (3u-2v)-\frac{2u^2}{v^2(3u-2v)}.$

b)

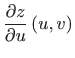$\displaystyle \frac{\partial z}{\partial u} \left( u,v\right)$	$\displaystyle = \frac{\partial z}{\partial x}\cdot \frac{\partial x}{\partial u... ...al y}\cdot \frac{\partial y}{\partial u}=yx^{y-1}\cdot 2u+x^y\ln x\cdot ve^{uv}$
	$\displaystyle =e^{uv}(u^2-v^2)^{e^{uv}-1}\cdot 2u+(u^2-v^2)^{e^{uv}}\ln (u^2-v^2)ve^{uv},$
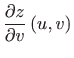$\displaystyle \frac{\partial z}{\partial v} \left( u,v\right)$	$\displaystyle = \frac{\partial z}{\partial x}\cdot \frac{\partial x}{\partial v... ...rtial y}\cdot \frac{\partial y}{\partial v}=yx^{y-1}(-2v)+x^y\ln x\cdot ue^{uv}$
	$\displaystyle = e^{uv}(u^2-v^2)^{e^{uv}-1}(-2v)+(u^2-v^2)^{e^{uv}}ue^{uv}\ln (u^2-v^2).$