Parcijalne derivacije funkcije dviju varijabli zadane implicitno

Odredite parcijalne derivacije prvog reda funkcije $\displaystyle z=f(x,y)$ zadane implicitno sa $\displaystyle x^2+y^2+z^2=1$ .

Rješenje.

Zadanu implicitnu jednadžbu ćemo zapisati u obliku $\displaystyle F(x,y,z)=x^2+y^2+z^2-1$ . Sada je $\displaystyle F_x=2x$ , $\displaystyle F_y=2y$ i $\displaystyle F_z=2z$ . Prema formuli za derivaciju implicitno zadane funkcije dviju varijabli [M2, definicija 3.13] slijedi

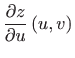$\displaystyle \frac{\partial z}{\partial x}\left( x,y\right)$	$\displaystyle = -\frac{x}{z},$
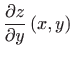$\displaystyle \frac{\partial z}{\partial y}\left( x,y\right)$	$\displaystyle = -\frac{y}{z}.$