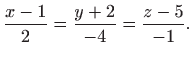☰
matematika2
Totalni diferencijal implicitno zadane
FUNKCIJE VIŠE VARIJABLA
Primjer primjene tangencijalnih ravnina
Tangencijalna ravnina i normala
Odredite tangencijalnu ravninu i normalu na plohu
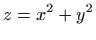 u točki
u točki
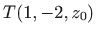 .
.
Rješenje.
Budući da točka 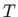 pripada zadanoj plohi vrijedi
pripada zadanoj plohi vrijedi
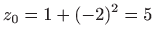 , tj. točka
, tj. točka 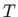 ima koordinate
ima koordinate
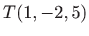 .
.
Prema fomuli za jednadžbu tangencijalne ravnine na plohu 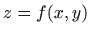 u točki
u točki
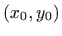
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 3.7]
[M2, poglavlje 3.7]
slijedi
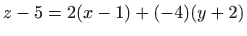 , , |
|
tj. tražena
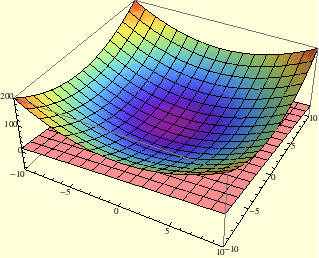
tangencijalna ravnina na zadani paraboloid (slika 3.6) ima jednadžbu
Slika:
Tangencijalna ravnina
na plohu
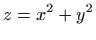 u točki
u točki
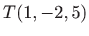
 |
Jednadžba normale na plohu 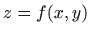 u točki
u točki
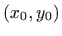 plohe dana je s
plohe dana je s
pa je tražena normala
Totalni diferencijal implicitno zadane
FUNKCIJE VIŠE VARIJABLA
Primjer primjene tangencijalnih ravnina
![]() u točki
u točki
![]() .
.
![]() pripada zadanoj plohi vrijedi
pripada zadanoj plohi vrijedi
![]() , tj. točka
, tj. točka ![]() ima koordinate
ima koordinate
![]() .
.
![]() u točki
u točki
![]()
![]() [M2, poglavlje 3.7]
[M2, poglavlje 3.7]
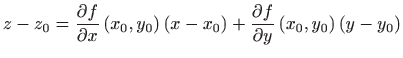
![]() u točki
u točki
![]() plohe dana je s
plohe dana je s