Totalni diferencijal implicitno zadane funkcije

Odredite totalni diferencijal prvog reda funkcije $\displaystyle z=f(x,y)$ zadane implicitno sa $\displaystyle x^2+y^2+z^2=a^2$ , je konstanta.

Rješenje.

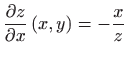Prema formuli za totalni diferencijal prvog reda funkcije dviju varijabli [M2, definicija 3.9] zaključujemo da moramo izračunati parcijalne derivacije funkcije $\displaystyle z$ . 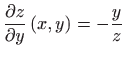Zapišemo li zadanu implicitnu jednadžbu u obliku $\displaystyle F(x,y,z)=x^2+y^2+z^2-a^2$ dobivamo $\displaystyle F_x=2x$ , $\displaystyle F_y=2y$ , $\displaystyle F_z=2z$ , odnosno $\displaystyle \frac{\partial z}{\partial x}\left( x,y\right)= -\frac{x}{z}$ i $\displaystyle \frac{\partial z}{\partial y}\left( x,y\right)=-\frac{y}{z}$ . Dakle, slijedi

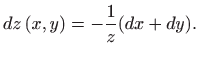$\displaystyle dz\left( x,y\right)=-\frac{1}{z}(dx+dy).$