☰
matematika2
Primjena ekstrema, 2. primjer
FUNKCIJE VIŠE VARIJABLA
Ekstremi na zatvorenom području,
Lokalni ekstremi funkcija triju varijabla
Izračunajte lokalne ekstreme funkcije
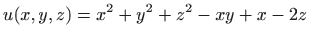 . . |
|
Rješenje.
Funkcija 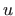 triju varijabla je beskonačno puta diferencijabilna na
triju varijabla je beskonačno puta diferencijabilna na
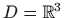 , a njene parcijalne derivacije prvog reda su
, a njene parcijalne derivacije prvog reda su
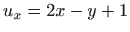 ,
, 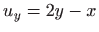 i
i 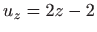 . Rješavanjem sustava
. Rješavanjem sustava
dobivamo
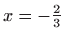 ,
,
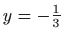 i
i 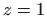 , što znači da je u
točki
, što znači da je u
točki
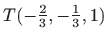 ispunjen nužan uvjet ekstrema
ispunjen nužan uvjet ekstrema
![[*]](../icons.gif/crossref.gif) [M2, teorem 3.7] pa je
[M2, teorem 3.7] pa je
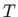 stacionarna točka funkcije
stacionarna točka funkcije 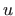 .
.
Provjerimo dovoljne
uvjete za postojanje lokalnog ekstrema funkcije 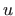 u točki
u točki 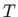 .
Izračunajmo najprije njene derivacije drugog reda.
.
Izračunajmo najprije njene derivacije drugog reda.
Dakle, u točki 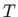 vrijedi
vrijedi
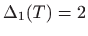 , , |
|
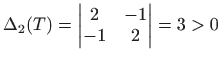 , , |
|
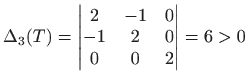 , , |
|
pa po teoremu
![[*]](../icons.gif/crossref.gif) [M2, teorem 3.8] zaključujemo da je
[M2, teorem 3.8] zaključujemo da je
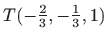 točka lokalnog minimuma funkcije
točka lokalnog minimuma funkcije 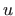 .
.
Primjena ekstrema, 2. primjer
FUNKCIJE VIŠE VARIJABLA
Ekstremi na zatvorenom području,
![]() triju varijabla je beskonačno puta diferencijabilna na
triju varijabla je beskonačno puta diferencijabilna na
![]() , a njene parcijalne derivacije prvog reda su
, a njene parcijalne derivacije prvog reda su
![]() ,
, ![]() i
i ![]() . Rješavanjem sustava
. Rješavanjem sustava
![]() u točki
u točki ![]() .
Izračunajmo najprije njene derivacije drugog reda.
.
Izračunajmo najprije njene derivacije drugog reda.
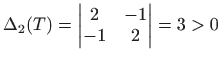 ,
,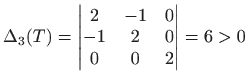 ,
,