☰
matematika2
Primjena vezanog ekstrema, 1.
FUNKCIJE VIŠE VARIJABLA
Zadaci za vježbu
Primjena vezanog ekstrema, 2. primjer
U ravnini 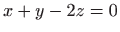 pronađite točku za koju je zbroj kvadrata udaljenosti od ravnina
pronađite točku za koju je zbroj kvadrata udaljenosti od ravnina 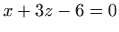 i
i 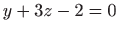 najmanji.
najmanji.
Rješenje.
Označimo s
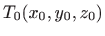 traženu točku. Udaljenosti točke
traženu točku. Udaljenosti točke 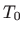 od dviju zadanih ravnina dane su respektivno s
od dviju zadanih ravnina dane su respektivno s
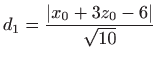 i i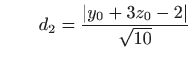 . . |
|
Prema tome, budući da koordinate točke 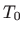 zadovoljavaju jednadžbu ravnine
zadovoljavaju jednadžbu ravnine 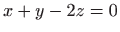 , Lagrangeova funkcija (
, Lagrangeova funkcija (
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 3.12]) je dana sa
[M2, poglavlje 3.12]) je dana sa
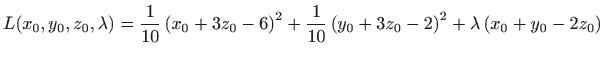 , , |
|
odnosno sa
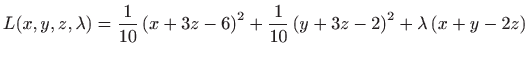 . . |
|
Nužan uvjet ekstrema glasi
Zbrojimo li prve tri jednadžbe, imamo
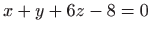 , , |
|
što zajedno s četvrtom jednadžbom daje
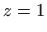 . . |
|
Oduzimanjem druge jednadžbe od prve dobivamo 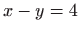 , što zajedno s četvrtom jednadžbom i
, što zajedno s četvrtom jednadžbom i 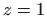 daje
daje
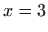 i i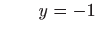 . . |
|
Dakle,
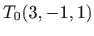 je tražena točka.
je tražena točka.
Primjena vezanog ekstrema, 1.
FUNKCIJE VIŠE VARIJABLA
Zadaci za vježbu
![]() pronađite točku za koju je zbroj kvadrata udaljenosti od ravnina
pronađite točku za koju je zbroj kvadrata udaljenosti od ravnina ![]() i
i ![]() najmanji.
najmanji.
![]() traženu točku. Udaljenosti točke
traženu točku. Udaljenosti točke ![]() od dviju zadanih ravnina dane su respektivno s
od dviju zadanih ravnina dane su respektivno s
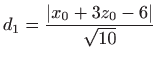 i
i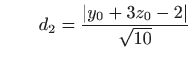 .
.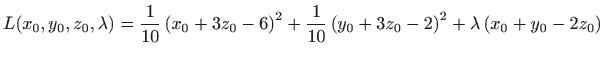 ,
,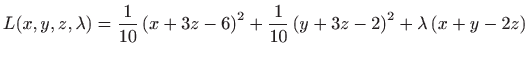 .
.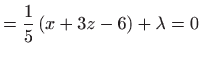 ,
,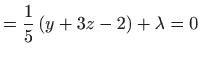 ,
,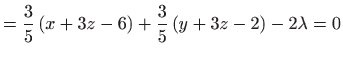 ,
,