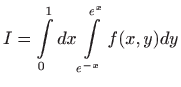 . . |
Nacrtajte područje integracije i promijenite redoslijed integriranja u integralu
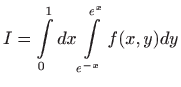 . . |
Područje integracije
![]() [M2, definicija 4.2] je dano s
(vidi sliku 4.1)
[M2, definicija 4.2] je dano s
(vidi sliku 4.1)
Prema
![]() [M2, napomena 4.1] i svojstvu V2 u
[M2, napomena 4.1] i svojstvu V2 u
![]() [M2,
poglavlje 4.1] smijemo zamijeniti
redoslijed integracije, odnosno integrirati prvo po varijabli
[M2,
poglavlje 4.1] smijemo zamijeniti
redoslijed integracije, odnosno integrirati prvo po varijabli ![]() .
U tom slučaju područje integracije rastavljamo na uniju dvaju disjunktnih
područja
.
U tom slučaju područje integracije rastavljamo na uniju dvaju disjunktnih
područja
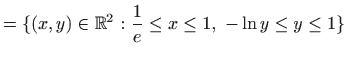 , , |
||
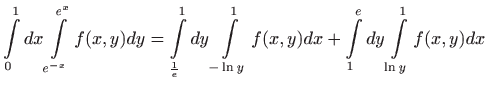 . . |