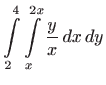 . . |
Promijenite redoslijed integriranja i izračunajte vrijednost integrala
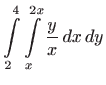 . . |
Rješenje.
Područje integracije grafički je prikazano na slici 4.2.
Promijenimo redoslijed integriranja. U tom slučaju integriramo po uniji dvaju područja (slika 4.3):
Izračunajmo vrijednost integrala uzastopnim računanjem dvaju jednostrukih
integrala uz pomoć Newton-Leibnitzove formule (
![]() [M2, poglavlje 2.2]):
[M2, poglavlje 2.2]):
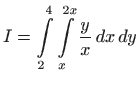 |
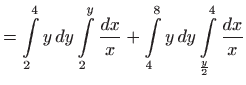 |
|
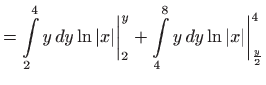 |
||
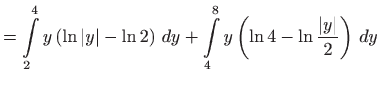 |
||
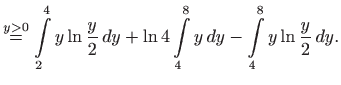 |
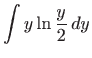 |
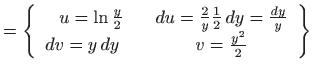 |
|
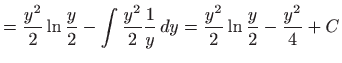 , , |
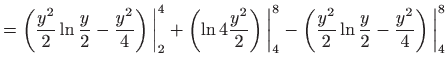 |
||