☰
matematika2
Neposredna integracija u trostrukom
VIŠESTRUKI INTEGRALI
Sferne koordinate u trostrukom
Cilindrične koordinate u trostrukom integralu
Izračunajte integral
ako je
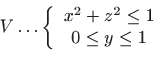 .
.
Rješenje.
Područje integracije 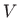 zadanog integrala prikazano je na slici 4.12.
zadanog integrala prikazano je na slici 4.12.
Slika:
Područje integracije zadano s
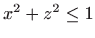 i
i
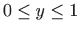 .
.
 |
Uvedimo cilindrične koordinate
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 4.3.1], ali tako da polarni koordinatni sustav bude u ravnini
[M2, poglavlje 4.3.1], ali tako da polarni koordinatni sustav bude u ravnini 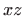 :
:
U novim koordinatama je element volumena jednak
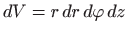 , , |
|
odnosno, Jakobijan je 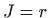 , pa je integral jednak
, pa je integral jednak
Neposredna integracija u trostrukom
VIŠESTRUKI INTEGRALI
Sferne koordinate u trostrukom
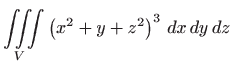
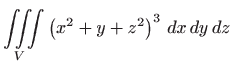
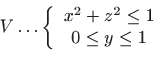 .
.
![]() zadanog integrala prikazano je na slici 4.12.
zadanog integrala prikazano je na slici 4.12.
![]() [M2, poglavlje 4.3.1], ali tako da polarni koordinatni sustav bude u ravnini
[M2, poglavlje 4.3.1], ali tako da polarni koordinatni sustav bude u ravnini ![]() :
:
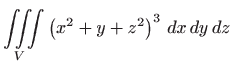
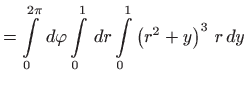
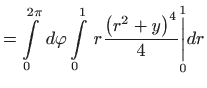
![$\displaystyle =\int\limits_{0}^{2\pi } d\varphi \int\limits_{0}^{1} \left[ \frac{1}{4}
r\left( r^{2}+1\right) ^{4}-\frac{1}{4}r^{9}\right] dr$](img1371.gif)
![$\displaystyle =\int\limits_{0}^{2\pi } \left[ \frac{1}{8}\frac{\left( r^{2}+1\...
...1}{4}
\frac{r^{10}}{10}\right] \underset{0}{\overset{1}{\bigg\vert}} d\varphi$](img1372.gif)
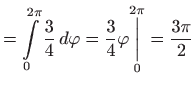 .
.