Odredite funkciju ![]() za koju funkcional
za koju funkcional
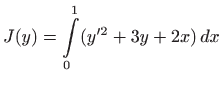
postiže ekstremnu vrijednost uz uvjete
Rješenje.
Uz oznaku
![]() vrijedi
vrijedi ![]() i
i
![]() .
Prema
.
Prema
![]() [M2, poglavlje 4.7], funkcija
[M2, poglavlje 4.7], funkcija ![]() zadovoljava
Euler-Lagrangeovu jednadžbu
zadovoljava
Euler-Lagrangeovu jednadžbu
![]() [M2, (4.6)]:
[M2, (4.6)]:
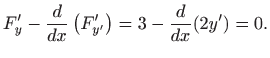
Dakle,
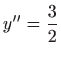 pa je
pa je
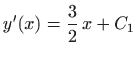 i
i
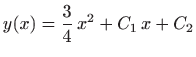 .
Uvrštavanje rubnih uvjeta daje
.
Uvrštavanje rubnih uvjeta daje 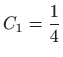 pa funkcional
poprima ekstremnu vrijednost za funkciju
pa funkcional
poprima ekstremnu vrijednost za funkciju
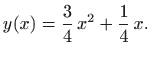
Vrijedi