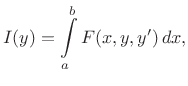
U ovom poglavlju objasnit ćemo osnove varijacijskog računa (ili računa varijacija), metode koja služi za modeliranje i rješavanje važnih matematičkih, fizikalnih i inženjerskih problema.
Problemi varijacijskog računa svode se na diferencijalne jednadžbe. Za bolje razumijevanje izlaganja u ovom poglavlju potrebno je poznavati neke tehnike za rješavanje diferencijalnih jednadžbi iz glave 5, no gradivo je izloženo na način da je ta potreba svedena na minimum.
Izrazom
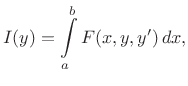
gdje je
Zadatak je
naći neprekidno derivabilnu funkciju ![]() za koju funkcional
za koju funkcional ![]() dostiže ekstremnu vrijednost (ako takva funkcija postoji).
Moguće je zahtijevati da funkcija
dostiže ekstremnu vrijednost (ako takva funkcija postoji).
Moguće je zahtijevati da funkcija ![]() zadovoljava i jedan ili oba
rubna uvjeta:
zadovoljava i jedan ili oba
rubna uvjeta:
Neka su
![]() koordinate materijalne točke u trenutku
koordinate materijalne točke u trenutku ![]() . Neka je
. Neka je ![]() prijeđeni put,
prijeđeni put, ![]() brzina i
brzina i ![]() masa materijalne točke. Konstantu gravitacije
označit ćemo s
masa materijalne točke. Konstantu gravitacije
označit ćemo s ![]() . Prema zakonu o očuvanju energije vrijedi
. Prema zakonu o očuvanju energije vrijedi
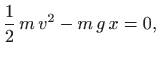
odnosno,
S druge strane je
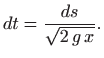
Prema poglavlju 2.6.2 element duljine luka jednak je
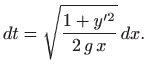
Integral daje ukupno vrijeme spuštanja:
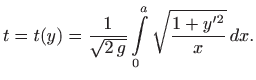
Dakle, brahistohrona je krivulja koja minimizira funkcional