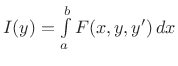 .
Neka je krivulja
.
Neka je krivulja
Neka je ![]() neprekidna dva puta derivabilna
funkcija svojih argumenata.
Pretpostavimo da je krivulja
neprekidna dva puta derivabilna
funkcija svojih argumenata.
Pretpostavimo da je krivulja
![]() ekstrem funkcionala
ekstrem funkcionala
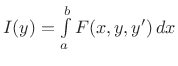 .
Neka je krivulja
.
Neka je krivulja ![]() blizu krivulji
blizu krivulji ![]() ,
odnosno neka za
,
odnosno neka za ![]() vrijedi
vrijedi
Razlika
Dakle, vrijedi
![]() . Ovu jednakost možemo zapisati i kao
. Ovu jednakost možemo zapisati i kao
gdje je
pa je
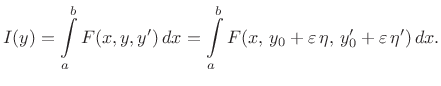
Ako fiksiramo
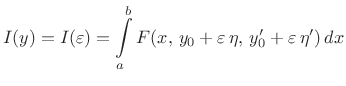
pa nužni uvjet ekstrema glasi
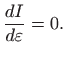
Funkcija
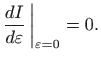
Prema pravilu za deriviranje pod znakom integrala (teorem 4.3) i pravilu za deriviranje složenih funkcija (teorem 3.5) vrijedi
![$\displaystyle \frac{dI}{d\varepsilon}= \int\limits _a^b \left[ \frac{\partial F...
...x,
y_0+\varepsilon \eta, y_0'+\varepsilon \eta') \eta' \right] dx.
$](img2419.gif)
Za
![$\displaystyle \frac{dI}{d\varepsilon} \bigg\vert _{\varepsilon=0}
= \int\limi...
... +
\frac{\partial F}{\partial y_0'}(x,
y_0, y_0') \eta' \right] dx=0.
$](img2423.gif)
Parcijalna integracija drugog člana uz
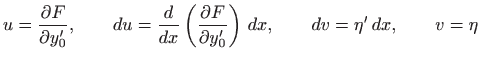
daje
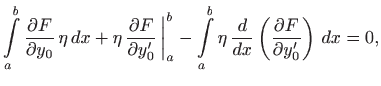
odnosno
Razlikujemo dva slučaja.
Slučaj 1.
Ako funkcija ![]() zadovoljava rubne uvjete
zadovoljava rubne uvjete ![]() i
i
![]() , onda u obzir dolaze samo one funkcije
, onda u obzir dolaze samo one funkcije ![]() koje također zadovoljavaju
iste rubne uvjete, odnosno za koje je
koje također zadovoljavaju
iste rubne uvjete, odnosno za koje je ![]() i
i ![]() . No, onda je očito
. No, onda je očito
![]() pa je prvi član u relaciji (4.4) jednak nuli te
nužan uvjet ekstrema glasi
pa je prvi član u relaciji (4.4) jednak nuli te
nužan uvjet ekstrema glasi
za neki
![$\displaystyle \eta(x)=\left\{ \begin{array}{ll}
0, & x\in[a,\bar x-\xi],\\
(x-...
...in(\bar x-\xi,\bar x+\xi),\\
0,& x\in[\bar x +\xi,\leq b].
\end{array}\right.
$](img2442.gif)
Funkcija
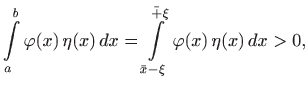
što je suprotno pretpostavki teorema i teorem je dokazan.
Direktnom primjenom teorema 4.5 na relaciju (4.5), uz ispuštanje indeksa 0 radi jednostavnosti, dobili smo Euler-Lagrangeovu jednadžbu
Slučaj 2.
Ako funkcija ![]() ne zadovoljava nikakve rubne uvjete, postupamo na
sljedeći način: relacija (4.4) vrijedi za proizvoljnu funkciju
ne zadovoljava nikakve rubne uvjete, postupamo na
sljedeći način: relacija (4.4) vrijedi za proizvoljnu funkciju
![]() pa i za takve za koje je
pa i za takve za koje je
![]() . Stoga zaključujemo da i u
ovom slučaju rješenje
. Stoga zaključujemo da i u
ovom slučaju rješenje ![]() mora zadovoljavati Euler-Lagrangeovu jednadžbu.
Međutim, sada i prvi član u relaciji (4.4) mora biti jednak nuli za
svaku funkciju
mora zadovoljavati Euler-Lagrangeovu jednadžbu.
Međutim, sada i prvi član u relaciji (4.4) mora biti jednak nuli za
svaku funkciju ![]() pa rješenje
pa rješenje ![]() mora zadovoljavati uvjete
transverzalnosti (poprečnosti)
mora zadovoljavati uvjete
transverzalnosti (poprečnosti)
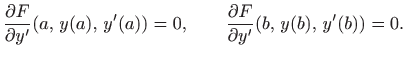
Moguća je kombinacija prethodnih slučajeva: ako je rubni uvjet zadan samo u jednom kraju, onda u drugom kraju mora biti zadovoljen uvjet transverzalnosti.
Dovoljne uvjete ekstrema
(Legendreovi uvjeti) navodimo bez dokaza. Neka
funkcija ![]() zadovoljava nužne uvjete ekstrema funkcionala
zadovoljava nužne uvjete ekstrema funkcionala ![]() . Tada
vrijedi:
. Tada
vrijedi: